Gli Speciali - La matematica del rumore

Benvenuti nell'approfondimento relativo al rumore in fotografia, o meglio alla matematica che si cela dietro il rumore fotografico. In questo lunghissimo articolo andremo ad analizzare le varie componenti del rumore, le fonti, le metodologie per la riduzione dello stesso, nonché tutti i modelli matematici che si celano dietro il rumore stesso. Le Fonti del rumore Rumore di lettura La luce è costituita da gruppi discreti di energia chiamati fotoni: più la luce è intensa, più è alto il numero di fotoni al secondo che illuminano la scena. Il flusso di fotoni avrà un flusso medio (numero al secondo) che arriva ad una determinata area del sensore. Rispetto a questo valore, ci saranno ovvie fluttuazioni intorno. Le leggi statistiche che regolano queste fluttuazioni sono chiamate statistiche di Poisson e sono Per maggiori dettagli potete visitare Wikipedia . Le fluttuazioni del numero di fotoni sono visibili nelle immagini come rumore: rumore di Poisson , chiamato anche rumore di fotoni. Un esempio di questo rumore è mostrato nella figura di seguito [caption id="attachment_11349" align="aligncenter" width="640"] Rumore di fotone in un'immagine del cielo. Nell'istogramma a destra, la coordinata orizzontale è il livello grezzo, l'asse verticale traccia il numero di pixel nel campione con quel livello grezzo. Il rumore del fotone è stato isolato prendendo la differenza di due immagini successive. I valori grezzi per ogni pixel quindi differiscono solo dalle fluttuazioni nel numero dei fotoni a causa delle statistiche di Poisson (a parte un contributo molto minore del rumore di lettura). 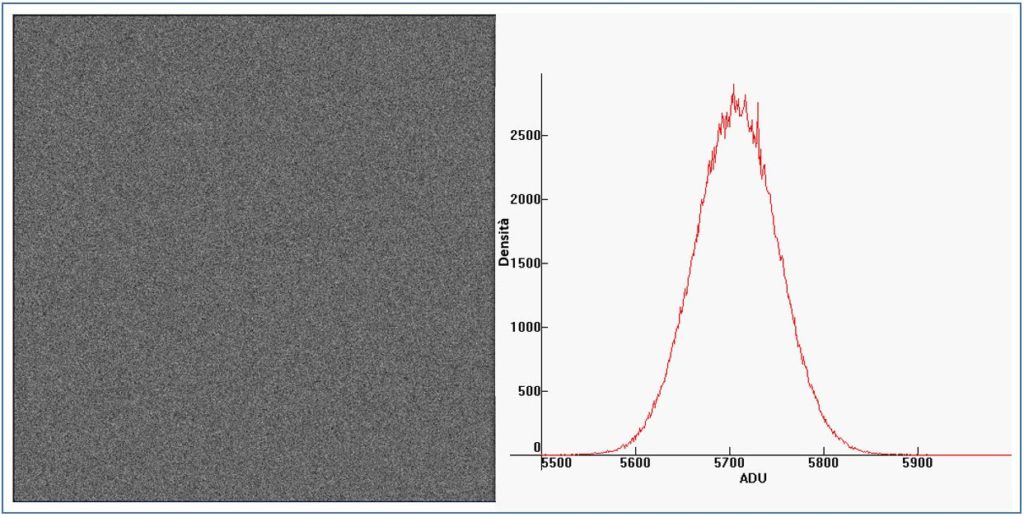[/caption] L'istogramma del rumore è essenzialmente una distribuzione gaussiana standard. La deviazione standard di questa curva a campana è la larghezza della campana. Le fluttuazioni dei conteggi di fotoni da pixel a pixel sono completamente non correlate. In termini di variazione spaziale, il rumore del fotone è un rumore bianco (in altre parole, ha uguale forza a tutte le frequenze spaziali) e ciò significa che ha un aspetto uniforme (punti bianchi e neri) senza struttura o motivo (ovvero casuale). Una caratteristica importante delle fluttuazioni che obbediscono alle statistiche di Poisson è che la loro deviazione standard (ovvero la tipica fluttuazione al di fuori della media nel conteggio tipico) è uguale alla radice quadrata del conteggio medio stesso. Cioè, se 10000 fotoni sono raccolti, la tipica fluttuazione sarà di circa 100, il che significa quindi che i conteggi di variano da circa 9900 a 10100. Se invece sono raccolti in media 100 fotoni, la variazione da considerare sarà +/- 10. Quindi, man mano che il segnale aumenta, anche il rumore del fotone aumenta, ma più lentamente. E il rapporto segnale-rumore aumenta come la radice quadrata del numero di fotoni raccolti. Maggiore è l'illuminazione, minore è il rumore nello scatto. Più è bassa l'illuminazione, più è evidente. Rumore del pattern In termini di variazione spaziale, il rumore di lettura non è del tutto bianco. A un esame più attento, vi sono schemi unidimensionali nelle fluttuazioni nella figura di sopra. Poiché l'occhio umano è adattato a percepire i pattern, questo pattern o rumore di banding può essere visivamente più evidente del rumore bianco, anche se comprende un contributo minore al rumore generale. Questo rumore è più evidente con macchine fotografiche più datate. [caption id="attachment_11351" align="aligncenter" width="640"] Rumore del pattern di una Canon 20D a ISO 800, esposizione 1/1000 e copriobiettivo inserito.Il rumore del pattern può essere rimosso creando un modello dalla media di 16 fotogrammi neri identici e sottraendola dall'immagine. [/caption] Il rumore del pattern può avere sia un componente fisso che non varia da immagine a immagine così come un componente variabile che, sebbene non casuale da pixel a pixel, non è lo stesso da immagine a immagine. Nell’immagine di sopra. Sono presenti sia bande orizzontali che verticali. Un modello per il rumore del modello fisso è stato creato utilizzando una media di sedici fotogrammi neri identici (da sottrarre all’immagine originale): questo ha l'effetto di eliminare qualsiasi componente fluttuante del rumore di lettura, lasciando principalmente il componente fisso. Effettuando la sottrazione, le bande verticali scompaiono in gran parte (vedi la seconda immagine delle due di sopra), lasciando solo il rumore variabile delle bande in direzione orizzontale, nonché un componente omogeneo (bianco) del rumore letto; la larghezza dell'istogramma del rumore di lettura diminuisce di circa il 20%. Ciò fornisce un'indicazione di come il rumore del pattern possa essere visivamente fastidioso: anche se il rumore del pattern fisso è solo del 20% circa del rumore complessivo, è piuttosto evidente perché la nostra percezione visiva tende ad individuare pattern o strutture di qualche genere. Rumore termico L'agitazione termica degli elettroni in un sensel può liberare alcuni elettroni. Questi elettroni termici sono indistinguibili dagli elettroni liberati dall'assorbimento del fotone (luce), e quindi provocano una distorsione del conteggio dei fotoni nei dati grezzi. Gli elettroni termici vengono liberati a una velocità relativamente costante per unità di tempo, quindi il rumore termico aumenta con il tempo di esposizione. Il grafico di seguito mostra la deviazione standard del valore grezzo di un in funzione del tempo di esposizione. 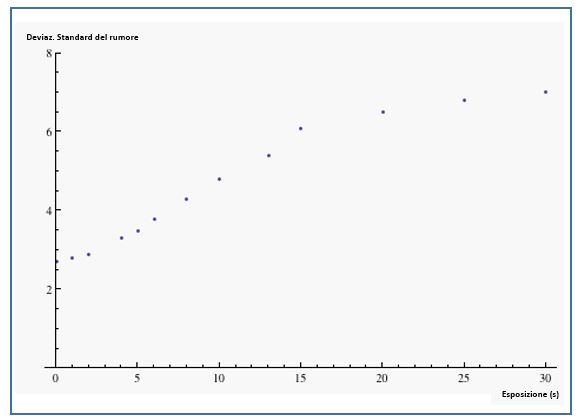Il livello di rumore aumenta in funzione del tempo di esposizione, con un incremento considerevoleal di sopra di un tempo di esposizione di circa 15 secondi in questo particolare campione (una Canon 20D). La causa di questo cambiamento di comportamento è che l'aumento della deviazione standard è in gran parte dovuto a pochi pixel "caldi" sulla coda della distribuzione. Quando i valori grezzi di questi pixel raggiungono 4095 (il valore massimo possibile per questa fotocamera), il loro contributo alla deviazione standard si satura e solo gli altri pixel contribuiscono a un aumento (più lento) della deviazione standard. Al fine di rendere visibile la crescita del numero di questi pixel "caldi", nella figura seguente sono evidenziati in bianco i pixel i cui valori sono quattro o più deviazioni standard sopra la media. [caption id="attachment_11353" align="aligncenter" width="640"] I pixel caldi sono i principali contributori al rumore termico. In bianco sono i pixel i cui valori sono quattro o più deviazioni standard sopra la media. A sinistra, il tempo di esposizione è 15 secondi; a destra, 30 sec[/caption] Un altro contributo termico alla degradazione dell'immagine è il bagliore dell'amplificatore , che è causato dalla radiazione infrarossa (calore) emessa dall'amplificatore di lettura Per esposizioni inferiori ad un secondo circa, il rumore di lettura è relativamente costante e il rumore termico costituisce un contributo trascurabile al rumore complessivo dell'immagine. PRNU Non-uniformità della risposta dei pixel (PRNU): non tutti i pixel di un sensore hanno esattamente la stessa efficienza nel catturare e contare i fotoni. Anche se non ci fossero rumori di lettura, rumore di fotoni e via discorrendo, ci sarebbe comunque una variazione nei conteggi grezzi da questa non uniformità nella risposta dei pixel, o PRNU. Il grafico di seguito mostra il "rumore" PRNU in funzione dell'esposizione. Il grafico è stato ottenuto misurando separatamente il rumore combinato del fotoni e il rumore di lettura e sottraendo in modo appropriato queste due componenti dal rumore totale in una serie di esposizioni. Questo rumore residuo è tracciato nel grafico. Il "rumore" PRNU aumenta in proporzione al livello di esposizione. I i diversi pixel registrano percentuali diverse dei fotoni incidenti su di essi, e quindi il contributo alla deviazione standard dei valori grezzi da PRNU aumenta in proporzione diretta al livello di esposizione. D'altra parte, il rumore dei fotoni aumenta come la radice quadrata dell'esposizione e leggere il rumore è indipendente dal livello di esposizione. Quindi il PRNU è il più importante a valori maggiori di esposizione: ad esempio, PRNU è maggiore degli altri rumori quando si scatta a valori di 2/3 EV o maggiori. AL contrario, a livelli di esposizione inferiori, il rumore dei fotoni è il contributo dominante fino a quando non si entra nelle ombre profonde dove il rumore di lettura diventa preponderante. Errore di quantizzazione Q uando il segnale analogico di tensione dal sensore viene digitalizzato in un valore grezzo, viene arrotondato a un valore intero vicino. A causa di questo arrotondamento, il valore grezzo indica un valore “impreciso” del segnale effettivo, un’imprecisione comunque piccola. L'errore introdotto dalla digitalizzazione è chiamato errore di quantizzazione ed è talvolta definito rumore di quantizzazione . Si tratta di un contributo piuttosto secondario al rumore, difficile da visualizzare La misurazione del rumore Il rumore di scatto Il rumore totale nei dati grezzi è una combinazione di tutte le fonti di rumore di cui prima. Le fonti di rumore indipendenti si combinano in quadratura, ovvero il quadrato del rumore totale è la somma dei quadrati dei singoli contributi. Le fonti di rumore più importanti per le esposizioni tipiche sono il rumore di lettura e il rumore dei fotoni. Insieme determinano il rapporto segnale / rumore disponibile per determinati parametri di esposizione e quindi la qualità dell'immagine. Combinato in quadratura, il rumore di lettura R e il rumore dei fotoni P determinano il rumore totale N come . Possiamo, per approssimazione, ignorare al momento gli effetti del rumore termico, PRNU o di quntizzazione in quanto molto più piccoli dei due presi in considerazione. Le statistiche di Poisson indicano che l'entità del rumore dei fotoni è la radice quadrata del numero di fotoni; se S’ è il numero di fotoni nel segnale, il numero tipico P' di fotoni attribuibili al rumore dello scatto è (P ') 2 = S' . Tuttavia, i dati grezzi dei pixel sono dati dal valore grezzo in ADU, piuttosto che direttamente in termini di fotoni. La costante di proporzionalità tra fotoni catturati e livelli grezzi è il guadagno g . Con g /livello grezzo, si ottiene il segnale S = S '/g e il rumore di scatto P = P'/g , dove S è il segnale in ADU e P è il rumore di scatto in ADU. Il guadagno è inversamente proporzionale all'impostazione ISO: se si raddoppia l'ISO e si dimezza l'esposizione, verranno catturati metà dei fotoni ma il valore grezzo rimane lo stesso. Così si ottiene . dove G è l'impostazione ISO e U è una costante (che differisce per i diversi modelli di fotocamera) conosciuta come guadagno unitario . Il risultato è che il segnale e il rumore di scatto misurati in ADU sono correlati da . Quindi, il rumore di lettura e il rumore dei fotoni contribuiscono come , dove N, R e S sono misurati a livelli grezzi (ADU). In conclusione : è possibile misurare sia il rumore di lettura R che il guadagno misurando il rumore nei livelli grezzi a vari livelli di esposizione, tracciando il quadrato del rumore rispetto all'esposizione e adattando il risultato a una linea retta. R è la radice quadrata dell'intercetta di questa linea, e g è l'inverso della sua inclinazione. Effetti sistematici come PRNU possono contaminare la misurazione del rumore di lettura e dei fotoni. Per eliminare questi effetti, è meglio misurare il rumore combinato di fotoni e di lettura prendendo la differenza di due immagini successive aventi lo stesso livello di esposizione. Gli effetti sistematici fissi si annullano tra le due immagini quando vengono sottratti, lasciando solo fluttuazioni la cui deviazione standard è la radice quadrata di 2, ovvero circa 1.414 volte il rumore combinato di lettura e rumore dei fotoni di una singola immagine (poiché il rumore si aggiunge in quadratura, il rumore di due immagini sommati insieme è . Una tabellone colorchecker uniformemente illuminato e leggermente sfocato fornisce un'immagine bersaglio adatta per fare questi esercizi, con ciascun quadrato che fornisce una patch uniforme in cui misurare il livello di rumore e segnale e quindi diversi punti dati da una singola immagine. Prendendo le immagini leggermente sfocate, si garantisce che eventuali imperfezioni superficiali del soggetto non forniscano un falso contributo alle misurazioni del rumore. In alternativa, è possibile riprendere coppie consecutive di immagini (completamente sfocate) di un muro vuoto, illuminato in modo uniforme. Anche il cielo blu senza nuvole è un buon soggetto. Per riassumere: Prendete un paio di immagini di un colorchecker uniformemente illuminato, leggermente fuori fuoco. Prendete la somma delle due immagini e separate il risultato nei suoi singoli canali di colore. Misurate il valore grezzo medio di ogni quadrato di colore in uno dei due sottocanali del verde dell’array di Bayer. Dividete per due per ottenere il segnale medio. Prendete la differenza tra le due immagini, divisa in canali di colore e misurate la deviazione standard in ogni quadrato di colore. Dividete per la radice quadrata di 2 per ottenere la somma del rumore di lettura e di scatto (rumore dei fotoni) per quel particolare quadrato di colore.. Disegnate il quadrato del rumore rispetto al segnale, adattandolo a una linea retta. L'intercetta è il quadrato del rumore letto, la pendenza è l'inverso del guadagno. 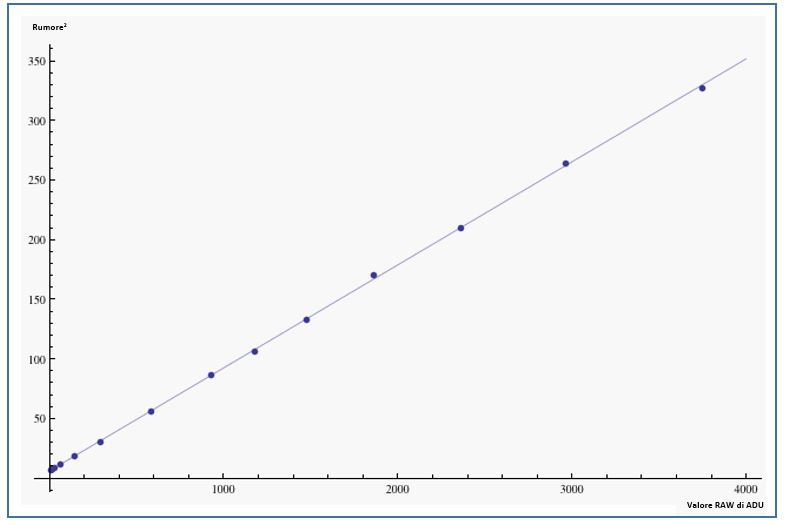I risultati per una Canon 20D sono mostrati nel grafico seguente Sulle reflex digitali Canon esiste un metodo alternativo per misurare il rumore letto. Canon applica un offset al segnale dal sensore: una tensione costante viene aggiunta al segnale dal sensore prima che il segnale sia quantizzato nell'ADC. Sebbene le fluttuazioni di tensione possono essere sia positive che negative, una quantità negativa verrà azzerata alla quantizzazione, poiché l'output dell'ADC deve essere un valore intero non negativo. Aggiungendo una tensione di offset, l'intero istogramma del rumore viene mantenuto, in quanto tutto l’istogramma viene spostato a destra, e quindi anche i valori negativi sono rappresentati (diventando positivi). [caption id="attachment_11357" align="aligncenter" width="588"] Se non ci fosse offset, i valori "neri" la gaussiana sarebbe accollata all’asse di sinistra, con la conseguente perdita di molta parte della gaussiana stessa. Nella figura di destra, quanto accade su una D300 Nikon: il valore di offset è zero e la gaussiana è tagliata. Questo rende molto più complesso il recupero del rumore. [/caption] PRNU La non uniformità della risposta dei pixel (PRNU) è un effetto aggiuntivo che può essere misurato tramite la stessa tecnica appena descrritta. La non uniformità risulta essere solo una frazione di una percentuale, e di conseguenza è giustificabile trattare questa variazione casuale nella risposta dei pixel come un'altra fonte di rumore da aggiungere in quadratura per leggere e rumore di ripresa: N 2 = R 2 + P 2 + W 2 dove W è il contributo di PRNU mente N , R e P sono rispettivamente il rumore totale, il rumore letto e il rumore dei fotoni. Ora, il PRNU è dovuto alle fluttuazioni della reattività dei pixel alla luce, e quindi le fluttuazioni che produce aumenteranno in proporzione diretta al livello di illuminazione S. In altre parole W = k S , dove k caratterizza la quantità di variazione nella reattività dei pixel. Il rumore di lettura e di scatto (fotoni) sono stati misurati sopra usando la differenza di due esposizioni identiche, in parte per eliminare gli effetti del PRNU. Una delle immagini di prova include gli effetti del PRNU e del rumore di lettura e di scatto mentre la seconda solo il PRNU. Va da se che la differenza delle immagini avrà solo il rumore di lettura e di scatto ma non il PRNU. Pertanto, per misurare la non uniformità della risposta dei pixel, si misura semplicemente la deviazione standard di uno dei due file utilizzati per determinare il rumore di lettura e di scatto e si sottrae (in quadratura) il contributo del rumore di lettura e di scatto precedentemente determinato: N 2 - (R 2 + P 2 ) = W 2 In conclusione : il PRNU dovrebbe essere lineare in funzione dell'esposizione, quindi tracciare i valori di W determinati da questa procedura rispetto ai corrispondenti valori grezzi S dovrebbe produrre una linea retta la cui pendenza k è la variazione frazionaria del guadagno dal pixel a pixel. È importante scegliere una zona del sensore relativamente priva di macchie di polvere per ottenere una buona misura (le macchie di polvere attenuano la risposta dei pixel al di sotto di esse e quindi contribuiranno a una non uniformità di risposta). Allo stesso modo, l'immagine di prova dovrebbe essere il più uniformemente illuminata possibile (e le misurazioni effettuate su aree di area abbastanza piccole) al fine di eliminare il più possibile gli effetti dei gradienti tonali attraverso l'immagine, che contribuiranno alla larghezza dell'istogramma (ma che non sono rumore). Fate riferimento alla figura seguente per un esempio Le fluttuazioni nella risposta da pixel a pixel sono date dalla pendenza n = 0.006 di questa curva. In altre parole, il PRNU è circa dello 0,6% per la fotocamera testata. Rapporto S/N vs. esposizione e Gamma dinamica Dopo aver misurato il rumore di lettura e il guadagno, è possibile tracciare il rapporto segnale / rumore ai vari ISO per avere un'idea della qualità dell'immagine in varie zone di esposizione e ai differenti valori di ISO. Al segnale S , il rumore combinato di lettura e di scatto sono Ad un livello basso di segnale, il rumore letto è più importante. Il rumore è approssimativamente costante e quindi S/N aumenta linearmente con il segnale. Ad un livello di segnale alto, il rumore del fotone (di scatto) è più importante, e quindi S/N aumenta come la radice quadrata del segnale. Un grafico di questo comportamento è mostrato nella figura 10 (per la fotocamera Canon 5D). Se tracciati su una scala log-log (ovvero in unità di stop per esposizione e S/N), l'aumento lineare a bassa esposizione produce una pendenza approssimativamente uguale a uno. C’è quindi un "ginocchio" nella curva, al di sopra del quale la relazione di radice quadrata tra segnale e rumore del fotone prende il sopravvento e la pendenza scende alla metà del valore. [caption id="attachment_11358" align="aligncenter" width="527"] Rapporto segnale / rumore vs. esposizione della canon 5D, per vari ISO. L'asse orizzontale è il valore grezzo (segnale) in EV. la coordinata orizzontale x corrisponde al valore grezzo S = 2 ^ x -1); (cioè, l'asse verticale è il rapporto S/N ai differenti stop (per S / N in dB, moltiplicato per sei). Solo il rumore di lettura e di scatto sono stati presi in considerazione. [/caption] Ricordiamo che il grafico tiene conto solo del rumore di lettura e del rumore sparato, ignorando il rumore del pattern e la non uniformità dei pixel, il rumore termico, e via discorrendo. Questi ultimi possono essere tranquillamente ignorati per tempi di esposizione inferiori a un secondo e ISO 400. Si noti inoltre che l'effetto visivo del rumore del pattern supera il suo contributo alle statistiche sul rumore e può portare a una qualità dell'immagine inferiore rispetto a quella suggerita dal rapporto S/N. Finora non abbiamo incluso PRNU nelle considerazioni sul S/N. In parte questo è dovuto al fatto che, al contrario del rumore di lettura e di scatto (che sono casuali), il PRNU è fisso ed è noto per un determinato sensore della fotocamera. Quindi può essere compensato semplicemente moltiplicando ciascun valore di pixel per un fattore di compensazione in base alla sua variazione di risposta misurata. Tuttavia, se non si adottano tali contromisure, PRNU pone un limite superiore al rapporto S/N. Poiché il rumore PRNU W è proporzionale al segnale S e quindi W = k S . e poiché il rumore totale N è maggiore del rumore W del PRNU, il rapporto S / N è limitato in alto (ovvero non può superare) da k . Ad esempio, prendendo in esempio la Canon 20D che presenta k = .006, il S/N ha il suo massimo al valore di In conclusione : l'inverso della pendenza del grafico PRNU è un limite superiore per il rapporto S/N, a meno che il PRNU non venga compensato in post-elaborazione. Il rapporto S / N è strettamente legato alla gamma dinamica (GD) della fotocamera. La gamma dinamica è il segnale massimo registrabile (il valore grezzo al quale il sensore si satura) diviso per il rumore letto, che è il segnale registrabile più basso. Il valore grezzo per la saturazione del sensore non può essere considerato come il massimo livello grezzo possibile e deve essere misurato (ad esempio sovraesponendo una scena con cinque o sei stop). Se prendiamo per esempio la Canon 40D a ISO 100, il sensore si satura a livello raw 13825 anziché al valore massimo disponibile di 16383 (14 bit). Il segnale massimo è quindi 13825-1024 = 12801 dopo aver sottratto l'offset bias scritto nei dati grezzi. Il rumore di lettura a ISO 100 è di 5,5 ADU, quindi la gamma dinamica è 12801 / 5,5 = 2327 ovvero 11,2 stop. Attnzione: non tutta la gamma dinamica teorica (calcolata) così ottenuta è utile nella pratica. La definizione di gamma dinamica presuppone che qualsiasi segnale sopra lo zero sia rilevabile e di qualità sufficiente. Tuttavia non esiste nella realtà una sola definizione, ma multiple: ciò che è utilizzabile da un osservatore (della foto) può essere inutile a un altro osservatore, essendo la “visione” di un’immagine molto soggettiva. Dobbiamo quindi partire dal presupposto che sia l’osservatore stesso a decidere autonomamente e a formulare il proprio standard per un GD utile. Al fine di spiegare meglio come funziona, prendiamo in considerazione la figura 11, creata ad hoc considerando tre fattori principali: Un gradiente tonale che copre 32 livelli nella scala 0-255 della profondità tonale a 8 bit. Testo con valore tonale uguale al minimo del gradiente. Rumore li lettura di una fotocamera (nel nostro caso la Canon 1D3) normalizzato per avere una deviazione standard uguale a quattro livelli. La differenza di contrasto tra il gradiente dello sfondo e il testo è il segnale, che sale da zero a 32 da sinistra a destra. Il rumore è un valore costante di quattro, quindi ogni 1/8 della larghezza dell'immagine rappresenta un aumento di S/N di uno (ovvero S/N = 0 a sinistra, 4 nel mezzo e 8 a destra). I segni bianchi in basso nella foto indicano i punti di incremento del S/N. Infine, i livelli sono stati ampliati di un fattore quattro e il contrasto migliorato allo scopo di facilitare la visualizzazione dell’immagine. Dopo aver deciso il minimo rapporto S/N accettabile per la propria vista, andate nella figura di cui sopra per determinare la gamma dinamica "utile"corrispondente. Individuate il valore grezzo in cui il rapporto S / N soddisfa la vostra soglia di accettabilità, quindi contate il numero di stop al livello grezzo di saturazione: questa è la gamma dinamica utile per voi. Ad esempio, supponiamo che il rapporto S/N minimo accettabile sia 4 = 2 2 . Sulla Canon 1D3, questo particolare rapporto S/N viene raggiunto con ISO 200 all'incirca con S = 2 4,4 ovvero 9,5 stop al di sotto del valore di saturazione di 13,9 (il valore massimo è leggermente inferiore a 2 14 -1 = 16383 a causa dell'offset di compensazione pari a 1024). Ad ISO 3200, lo stesso esercizio fornisce un DR utile di circa 7,1 stop. Rumore di lettura al variare del valore ISO Il rumore di lettura aumenta con l’aumentrare del valore ISO, poiché qualsiasi rumore aggiunto dalla lettura del sensore prima dell'amplificazione ISO viene amplificato dall'amplificatore di guadagno ISO. Un modello grezzo della variazione del rumore di lettura in funzione degli ISO è quindi quello di assumere fonti di rumore pre e postamplificazione indipendenti, che vengono combinate come in quadratura: Qui R è il rumore totale letto; R 0 è il rumore proveniente dai componenti del circuito a monte dell'amplificatore ISO il cui guadagno è pari a G. R 1 è il rumore generato dai componenti del circuito a valle dell'amplificatore ISO. 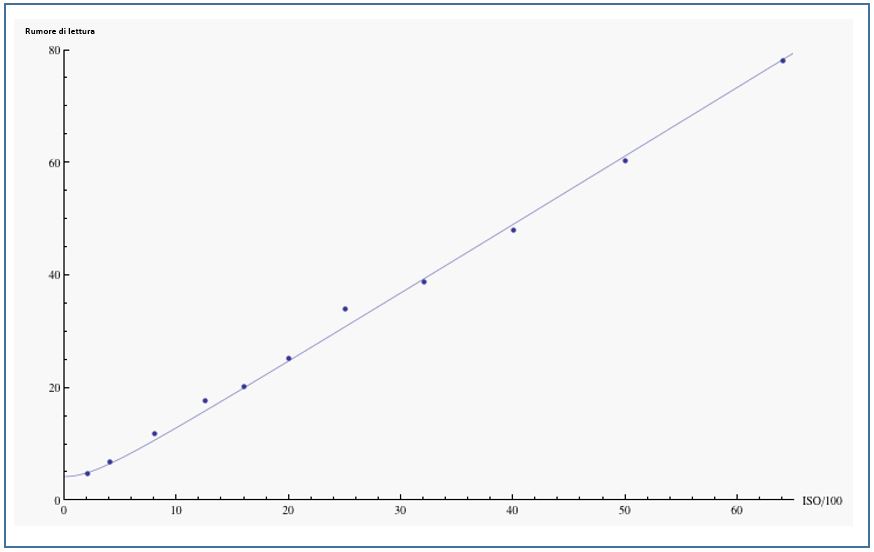Utilizzando questo modello per la Nikon D3, si ottiene in grafico di cui sotto Se le fotocamere Nikon utilizzando un singolo amplificatore a guadagno variabile per implementare tutte le impostazioni ISO, le Canon usano un approccio leggermente differente, utilizzando un sistema di amplificazione a due stadi: un amplificatore per l'ISO "principale" (100-200-400-800-1600-...) e un'amplificazione di secondo livello per implementare l'ISO "intermedio" (125-250-500-1000-... oppure 160-320-640-1250-...). Il primo amplificatore amplifica il rumore in ingresso e aggiunge del rumore, il secondo amplificatore amplifica i rumori combinati e quindi aggiunge un ulteriore rumore. Combinando tutti i rumori in quadratura, la naturale estensione del modello di rumore di lettura per due stadi di amplificazione è quindi dove G 2 = 1, 1,25, 1,60 è il guadagno che genera gli ISO intermedi dagli ISO principali e G 1 = 100, 200, 400, 800, 1600, ... sono i guadagni ISO principali (l'ordine delle amplificazioni potrebbe essere invertito, ma tale disposizione risulta non adatta ai dati). 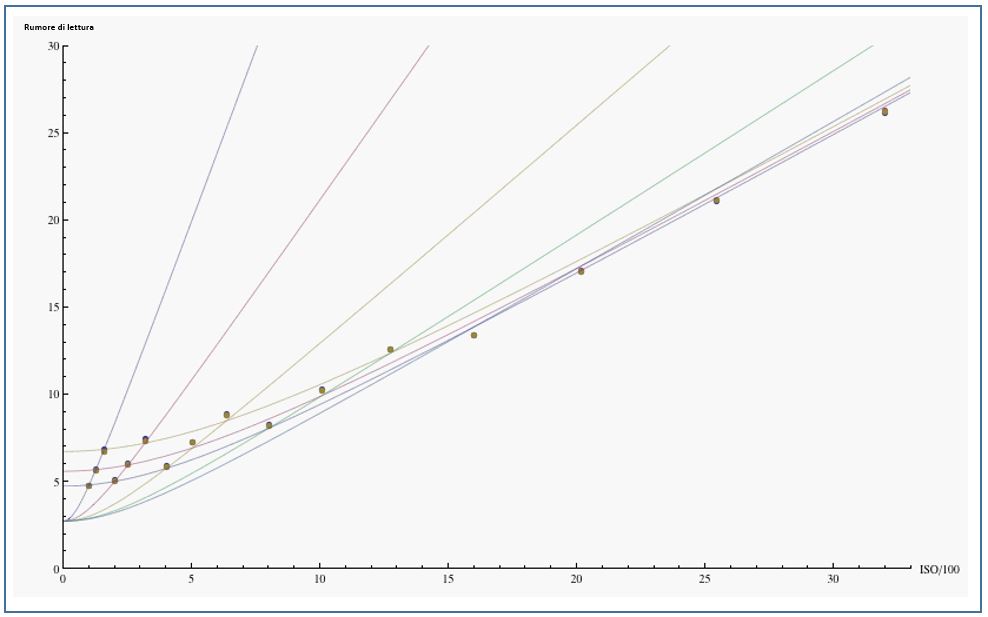Mettendo i risultati su di un grafico, si ottiene (Canon I3D): Va comunque puntualizzato che i modelli Canon di fascia bassa non eseguono l'amplificazione analogica per gli ISO intermedi ma sono ottenuti da una moltiplicazione dei dati grezzi nel software dopo la quantizzazione. Questo permette di avere un solo amplificatore (come con Nikon). I parametri di adattamento per il modello di amplificazione a due stadi utilizzato nei grafici sono Modello

R 0

R 1 R 2 1D3 (14 bit) 0,82 x 10 -2 3.9 2.7 4.7

Per gli ISO principali, l'ultima colonna della tabella combina (in quadratura) i contributi al modello dal rumore a valle dell'amplificazione ISO principale. In tutti i casi, il rumore a valle domina il rumore letto a ISO bassi e il rumore a monte R 0 fornisce il contributo principale per leggere il rumore ad alti ISO. L'amplificazione a due stadi utilizzata da Canon fornisce un po' più di informazioni su quale parte del rumore di lettura può essere attribuita a diversi componenti del circuito nelle sue fotocamere di fascia alta. Grazie al secondo stadio dell'amplificazione, si hanno informazioni separate su quanto del rumore letto è dovuto al rumore nell'amplificazione dell’ISO principale e quanto è legato all'amplificazione secondaria. Dalla tabella di sopra si vede che il rumore dominante a ISO basso deriva dal rumore dell'amplificatore ISO principale R 1 , con un minore contributo di R 2 (dovuto ai componenti a valle di questo amplificator)e e un contributo trascurabile dal rumore di lettura del sensore R 0 . Gli amplificatori a basso rumore migliorerebbero il rumore di lettura a basso ISO e comporterebbero un più alto range dinamico a ISO bassi. Dal grafico ci si rende conto anche che, per un valore ISO tra 1600 e 3200, cessa di esistere una differenza, in termini di rumore, tra amplificazione hardware e amplificazione software. Ovvero, nel caso della 1D3, il rumore di lettura 26.2 ADU a ISO 3200 è quasi il doppio del valore 13.4 ADU a ISO 1600. A questo punto non ha senso, nel caso di ISO 6400, usare un’amplificazione hardware ma conviene lavorare sul software, in quanto il il rumore letto sarà esattamente lo stesso ma la sua “moltiplicazione” sarà un’estrapolazione matematica che aggiungerà un rumore “standard” che non crescerà di una componente aggiuntiva dovuto all’amplificatore. Ciò significa anche che, se si scatta in formato RAW, ha poco senso usare gli ISO estesi poiché sono semplicemente manipolazioni matematiche dei dati grezzi in fase di post-acquisizione, e il loro effetto principale è quello di gettare via uno o più stop nei chiari. L'impostazione dell'amplificazione ISO analogica più elevata mantiene il margine di sicurezza al fine di non perdere informazioni. In aggiunta, essendo un’amplificazione software, la possiamo sempre eseguire in fase di post produzione sul nostro computer. Perché quindi perdere informazioni preziose? La riduzione del rumore La riduzione del rumore dei dati grezzi Esistono due ampie categorie di riduzione del rumore: Metodi di riduzione del rumore tramite la rimozione di effetti noti a livello di singoli pixel.Tali effetti includono il rumore del pattern fisso, la non uniformità di risposta dei pixel, il rumore di reset dei pixel e, in parte, il rumore termico. I contributi al rumore complessivo dell'immagine da queste fonti possono essere corretti misurando il rumore e sottraendolo. La misurazione e la correzione del rumore devono essere eseguite nello stato grezzo, ovvero quando i singoli dati dei pixel sono ancora intatti. Le correzioni non invocano alcun tipo di filtraggio che permetta di ridurre il rumore per una risoluzione ridotta, una saturazione dei colori ridotta, ecc. In breve, non ci sono effetti sull’immagine finale a causa di queste riduzioni del rumore. Altre forme di riduzione del rumore che comportano il filtraggio vengono anche eseguite in alcuni casi da alcuni modelli di fotocamera e prima che i dati del sensore vengano scritti sulla scheda di memoria.Gli esempi includono una riduzione del rumore ISO elevata (su alcuni modelli Sony) o una riduzione del rumore a lunga esposizione (su modelli Nikon). Questo tipo di correzione è invasiva, e la non disattivabilità preclude all'utente l'utilizzo di procedure NR più efficaci in fase di post-elaborazione, o anche la possibilità di scegliere se fare o meno NR. I metodi di riduzione del rumore del primo tipo migliorano il rapporto S/N senza calcolare la media dei pixel vicini, quindi migliorano la qualità dell'immagine con poche o nessuna conseguenza indesiderata. La seconda categoria di metodi consente di ridurre il rumore attenuando l'area di un pixel e degradando quindi alcuni aspetti dei dati del sensore. Esistono diversi metodi di riduzione del rumore che rientrano nella prima classe: Doppio campionamento correlato (CDS): Sottrazione del rumore del pattern Compensazione PRNU (nota anche come correzione del campo piatto ) Sottrazione dark frame Doppio campionamento correlato Il Doppio campionamento correlato (a volte indicato come "NR su chip"): in preparazione di una nuova esposizione, gli elettroni catturati nei fotositi dall'esposizione precedente devono essere eliminati dal sensore. Ogni fotodiodo deve essere resettato ad uno stato di esposizione zero. Se questo processo non è completamente efficace, potrebbero esserci elettroni residui presenti nel fotodiodo prima della successiva esposizione, e questi elettroni elimineranno il conteggio dei fotoni da questa nuova esposizione. Le fluttuazioni nel numero di elettroni presenti dopo aver azzerato il fotodiodo costituiscono il rumore di reset . Un vantaggio dei sensori CMOS è la loro capacità di leggere lo stato dei pixel in modo non distruttivo: lo stato del sensore (il suo conteggio di elettroni) può essere letto senza influire sugli elettroni, ovvero senza modificarne il numero. Questa funzione può essere utilizzata per eliminare il rumore di reset. Vediamo come. Dopo che il sensore è stato ripristinato (dall'esposizione precedente), viene letto lo stato del sensore, fornendo un conteggio degli elettroni residui (rumore di reset) e lasciando gli elettroni nella loro posizione posizione. Dopo la nuova esposizione, il sensore viene nuovamente letto, il risultato della lettura è la somma degli elettroni residui della precedente esposizione più gli elettroni catturati dalla nuova esposizione. Facendo la differenza delle due letture si ottiene il conteggio delle foto-elettroni dell'esposizione e quindi si sottrae il rumore di reset. Questa doppia lettura è nota come doppio campionamento correlato (CDS). Sui sensori CCD, gli elettroni devono essere estratti dal fotodiodo e trasferiti sul bordo del sensore per eseguire la lettura. I CDS possono essere eseguiti in questo circuito di lettura per colonna piuttosto che separatamente all'interno di ciascun fotodiodo. La doppia lettura aggiunge tempo alla lettura quando viene eseguita in serie sul bordo del sensore piuttosto che in parallelo su ciascun fotodiodo. Il CDS è una caratteristica della maggior parte dei sensori CMOS attuali, mentre, per il problema delle tempistiche (e della distruttività della lettura) non è implementato sui CCD. Sottrazione del rumore di lettura Alcune forme di rumore sono immutabili da immagine a immagine. Un esempio è il componente di rumore a pattern fisso del rumore di lettura. Poiché questo rumore è immutabile da un'immagine all'immagine, è necessario sviluppare un modello “master” rappresentante il disturbo in questione, ovverosia un file di immagine che contiene solo il rumore del pattern. Facendo la differenza di un'immagine grezza e del modello master di rumore, si può rimuovere completamente il rumore del pattern. Ma come si costruisce un modello contenente solo il rumore del pattern e nient'altro? Dopotutto, nessun file raw includerà solo il rumore del pattern ma conterrà anche ogni altro tipo di rumore di cui abbiamo visto nelle lezioni precedenti. Il punto è che altre forme di rumore di lettura variano da un'immagine all'altra. La “fortuna” è che se mediamo queste differenti componenti, si annullano tra di loro (non del tutto ma è una buona approssimazione), lasciando solo il rumore del pattern. In pratica, invece di mettere insieme i valori grezzi dei pixel vicini sulla stessa immagine, si raccolgono i valori grezzi dello stesso pixel su diverse immagini di rumore di lettura dell’immagine nera. Poiché il rumore del pattern fisso è immutabile da immagine a immagine, il suo contributo al totale aumenta in proporzione diretta al numero di immagini nere aggiunte insieme. D'altra parte, i rumori variabili oscillano su e giù e si combinano in quadratura perché variano in modo indipendente da immagine a immagine. Il risultato è che, sommando M immagini , il rumore del pattern è aumentato di un fattore M , mentre i rumori variabili salgono solo della radice quadrata di M. Dividendo per M al fine di ottenere un valore medio, il rumore del pattern ha il suo valore originale, mentre il componente di rumore fluttuante scende di un fattore sqrt [M] , ovverosia trascurabile rispetto a M . Si noti che la costruzione di un modello master per di rumore di lettura è sostanzialmente più difficile per le fotocamere ( ad esempio Nikon) che non includono un offset prima di scrivere i dati grezzi. Tutte le fluttuazioni del rumore negativo vengono troncate a zero e quindi le fluttuazioni casuali negative non vengono considerate quando si sommano più immagini nere tra di loro, il che rende il contributo del rumore maggiore. Nelle fotocamere in cui è considerato un offset, invece, i valori negativi vengono traslati nell’asse positivo e quindi vanno a fare media, rendendo piccolo il contributo (caso Canon). Avendo in mano il modello master del rumore del pattern (dovrebbe essere costruito un modello per ogni valore ISO, poiché il rumore di lettura cambia con ISO), può essere sottratto da qualsiasi immagine al fine di rimuovere la componente fissa del rumore del pattern. La componente variabile R del rumore letto aumenterà leggermente (di una quantità R/M ) in quanto la componente residua del rumore del pattern ed la componente variabile del rumore di lettura si combinano in quadratura. Da notare che più immagini sono raggruppate per formare il modello, più piccolo è questo effetto. In pratica una decina di fotogrammi sono sufficienti per fare un buon modello e ridurre quasi a zero questa componente. Compensazione del PRNU Una procedura simile a quella appena discussa può in teoria compensare la non uniformità della risposta dei pixel, anche se in pratica probabilmente non ne vale la pena. Il PRNU è come un rumore a schema fisso in quanto è una proprietà fissa del sensore che non cambia da immagine a immagine. Il PRNU, però, ha una sostanziale differenza: ovvero la forza del PRNU varia a seconda dell'esposizione. Poiché il PRNU è la più importante fonte di rumore a bassa sensibilità ISO e alta esposizione, è meglio isolarla scattando le immagini con il valore ISO più basso e esponendo tra 1/2 a 1 stop dal valore di saturazione del sensore. Il più grande “concorrente” del PRNU in questa situazione è il rumore di scatto. Quest’ultimo è un rumore casuale , e quindi il rumore di scatto viene eliminato da un modello PRNU facendo una media del numero M dei cosiddetti campi piatti . Un'esposizione a campo piatto è un'immagine di una superficie senza dettagli (ad esempio un muro bianco) illuminata uniformemente. Prendendo la media M tali immagini, il rumore di scatto (variabile) si riduce rispetto al PRNU fisso di un fattore radice quadrata di M . È importante che l'illuminazione sia il più uniforme possibile (in particolare, nessun dislivello) oppure la correzione introdurrebbecambiamenti tonali nell'immagine. E’ anche utile avere tutti e tre i canali di colore verso il bordo destro dell'istogramma in modo tale che il PRNU superi sostanzialmente il rumore di scatto in tutti i canali di colore. Infine, le immagini a campo piatto includono anche la vignettatura dell’obiettivo, una cosa che proprio non ci va bene. Questo effetto può essere mitigato fermando l'obiettivo un paio di stop prima il massimo, al fine di rendere l’immagine realmente uniforme. Le macchie di polvere sono un altro contaminante, quindi il sensore dovrebbe essere il più pulito possibile. Il PRNU è dovuto alla variazione in risposta alla luce da pixel a pixel. Ogni pixel ha un guadagno leggermente diverso. L'immagine del campo piatto è quindi una mappa della variazione del guadagno. Quindi, se prendiamo un'immagine e dividiamo i suoi valori grezzi dei (pixel per pixel) per i corrispondenti valori grezzi del campo piatto (qualcosa che può essere fatto ad esempio nel software di astrofotografia IRIS ) la variazione di guadagno si annullerà, e il PRNU verrà rimosso. Questa procedura ha una controindicazione da correggere: essa finirà anche per dividere i valori dei pixel per il livello di illuminazione medio dell'immagine del campo piatto, e quindi per ripristinare il livello di illuminazione originale sull'immagine corretta si dovrebbe moltiplicare per il livello di illuminazione medio L dell'immagine del campo piatto. Infine, per le fotocamere con un offset di polarizzazione del nero ( ad esempio 1024 su file RAW per le Canon a 14 bit), l'offset deve essere rimosso sia dall'immagine che dal campo piatto prima di eseguire la divisione. L’equazione corretta per rimuovere il PRNU è quindi: immagine corretta = L * (immagine - offset) / (campo piatto - offset) Volendo, si può sostituire la costante offset con il modello master del rumore di lettura, al fine di eliminare il rumore del pattern contemporaneamente. Sottrazione dell'immagine scura (per rumore termico) In situazioni in cui è presente un notevole rumore termico, in genere nelle lunghe esposizioni, può essere utile tentare di sottrarre il contributo del rumore termico dall'immagine. La procedura è simile a quella che abbiamo visto nelle precedenti lezioni riportata: scattate diverse immagini scure con lo stesso tempo di esposizione e la stessa temperatura operativa del file immagine (poiché la quantità di rumore termico aumenta con il tempo di esposizione e la temperatura operativa) e mediatele insieme (anche photoshop permette di fare questa operazione, se cercate uno strumento adatto). Il modello di rumore termico risultante consisterà in gran parte di rumore termico (e anche rumore di lettura a schema fisso) e, quando sottratto dall'immagine, gli effetti di rumore termico (in particolare l'amplificazione dell'amplificatore nelle esposizioni lunghe) saranno mitigati. Questa è esattamente la procedura che viene eseguita dalla fotocamera quando è abilitata la riduzione del disturbo da lunga esposizione (LENR). Dopo l'esposizione, la fotocamera mantiene l'immagine grezza in un buffer di memoria mentre una seconda esposizione scura (a tendina chiusa) viene presa con la stessa durata di scatto. L'immagine nera risultante viene sottratta dall'immagine memorizzata e quindi scritta nella scheda di memoria. Può essere piuttosto scomodo dover aspettare mentre la fotocamera riprende essenzialmente la stessa immagine scura per ogni esposizione. In pratica si impiega metà del tempo in attesa che la fotocamera completi l’acquisizione dei fotogrammi scuri. È più efficiente prendere una serie di fotogrammi scuri dopo aver realizzato lo sessione fotografica, per ogni tempo di posa utilizzato nella sessione stessa. In questo modo avrete un insieme di fotogrammi scuri master che possono essere utilizzati per molte immagini. Inoltre, il LENR nella fotocamera utilizza solo un singolo scatto la sottrazione: se questo va bene a rimuovere il rumore termico dall'immagine, il rumore di lettura, non essendoci media tra varie immagini, non viene tolto del tutto. Filtraggio in camera dei dati grezzi T utti i metodi di riduzione del rumore sopra citati comportano manipolazioni a livello dei singoli pixel. Nessun metodo effettua una comparazione tra pixel vicini al fine di eliminare il rumore. Questi metodi sono quindi molto diversi da ciò che viene convenzionalmente chiamato riduzione del rumore nell'elaborazione delle immagini. I programmi di riduzione del rumore come Noise Ninja , Neat Image , così come i filtri di rumore (il filtro mediano in Photoshop, per esempio) agiscono confrontando e facendo la media dei pixel vicini per ridurre l'aspetto del rumore. Questa forma di filtraggio del rumore viene talvolta applicata anche ai dati grezzi, in genere per esposizioni lunghe o immagini a ISO elevati in cui il rumore può essere problematico. Un esempio di questo tipo di filtro applicato ai dati grezzi prima che venga scritto si verifica con immagini a ISO elevate su alcuni modelli Sony. Rendersi conto di questo tipo di filtraggio non è facile, ma cè un modo abbastanza agevole: bisogna esaminare una patch tonale uniforme di un'immagine e vedere quanto rumore è presente alle diverse scale spaziali. Il rumore è il salto casuale intorno ai valori dei pixel di una quantità tipicamente compresa tra -N e + N , dove N è la grandezza del rumore. Per la maggior parte, il salto casuale avviene indipendentemente per ciascun pixel. Come abbiamo detto in precedenza, soprattutto nella sezione del rumore di scatto, la dipendenza spaziale dal rumore di scatto (e dalla dipendenza spaziale del componente più grande del rumore di lettura) è quella del rumore bianco, ovvero fluttuazioni di uguale magnitudine a tutte le frequenze spaziali. Ciò significa che i salti tra un pixel e il suo vicino sono grandi quanto i salti tra il pixel e vicino del suo vicino, ed il vicino del vicino del suo vicino e così via. Un esempio di rumore che non è bianco è il rumore delle bande; per esempio, nel rumore di bande orizzontale (vi rimando alle lezioni sulle fonti di rumore) se un pixel è un po' più luminoso della media, è probabile che i pixel fino ad una considerevole distanza nella stessa riga del sensore siano tutti un po' più luminosi della media, mentre i pixel vicini nella direzione verticale hanno valori non correlati. I filtri per la riduzione del rumore agiscono in maniera logica, confrontando i pixel vicini e cercando di ridurre l'entità del salto casuale dei loro valori con i pixel vicini. Dopo il filtraggio, i valori dei pixel vicini sono più simili tra di loro, mentre la differenza del valore tra un pixel e quelli più lontana (non essendo stata filtrata) rimane più o meno la stessa di prima. Il risultato è che il filtro del rumore in genere rimuove le fluttuazioni dei valori dei pixel su piccole scale, lasciandole in gran parte intatte a grandi scale. Questo effetto può essere reso visibile esaminando la trasformata di Fourier dell'immagine. La trasformata di Fourier (FT) è una rappresentazione dei dati dell'immagine per scala spaziale piuttosto che per posizione spaziale sul sensore (che è ovviamente il modo in cui il sensore la registra). Volendo porlo in grafico, l'effetto della riduzione del rumore sarà una diminuzione dell'ampiezza del rumore sulle scale più piccole. Un esempio è nella figura di seguito [caption id="attachment_11629" align="aligncenter" width="640"] La trasformata di Fourier di un'immagine di un muro bianco. L’area bianca che spunta dal centro indica come lo spettro del rumore ad alta frequenza è piatto fino al livello dei pixel ed è un'indicazione di una correlazione minima nelle fluttuazioni dei pixel vicini. Nella figura di destra, viene rappresentata la stessa trasformata di Fourier sulla quale è stato applicato un filtro mediano: l'oscuramento verso i bordi è il segno dello smorzamento dello spettro del rumore ad alta frequenza spaziale, dovuto alla media dei pixel adiacenti (una “sbavatura” dovuta alla riduzione del rumore, in parole povere). [/caption] Per ottenere la trasformata di Fourier di cui sopra, si è partiti da un’immagine di una parete bianca uniformemente esposta con ISO 200, e si è applicata una trasformata di Fourier del canale verde sia prima che dopo l'applicazione di un lieve filtro adattivo del rumore mediano. L’FT pone alte frequenze spaziali (piccole scale spaziali o effetti a livello di pixel) ai bordi dell’immagine. Gli effetti a piccola frequenza spaziale (grandi scale spaziali, o effetti uniformi su tutta l'immagine) appaiono al centro dell’immagine. Nell'immagine originale, la trama FT è uniforme rispetto al centro, indicando uno spettro di rumore quasi bianco (la zona luminosa al centro è dovuta ad una lieve sfumatura della luminosità della parete fotografata; le linee verticali e orizzontali che passano attraverso il centro dell’immagine sono indicazioni di una struttura monodimensionale, ovvero il rumore di banding). L'effetto di una filtro mediano lieve è presente nell’immagine a destra, dove l'oscuramento verso i bordi dell'immagine filtrata dal rumore è un'indicazione che il rumore è stato ridotto a scale spaziali fini, ma non è stato modificato su scale più grandi. I problemi dei software disponibili per la riduzione del rumore Sfortunatamente, nessuno dei metodi di riduzione del rumore sopra descritti può essere convenientemente applicato alle immagini raw utilizzando convertitori raw commerciali come ACR , DPP, Capture NX, Capture One, Bibble, Aperture , ecc. I metodi prevedono la preparazione di un modello di riduzione del rumore che deve quindi essere applicato all'immagine non elaborata prima della conversione. Nessuno dei convertitori raw in commercio ha la capacità di applicare un tale modello (il convertitore freeware dcraw può implementare una semplice sottrazione di frame neri, ma non metodi più sofisticati come la divisione per un campo piatto). Il tool IRIS può eseguire le manipolazioni desiderate sui dati grezzi, ma la sua gestione del colore è carente e i suoi algoritmi di demosaicing non sono i più sofisticati. Inoltre, l'uso di tecniche sofisticate di riduzione del rumore non dovrebbe limitare la scelta del convertitore grezzo dopo che è stata eseguita la riduzione del rumore. Ciò che sarebbe estremamente utile è un'applicazione software che consentirebbe di reinserire i dati di immagine processati dal rumore ma non convertiti in un formato grezzo, in modo che poi i convertitori standard potrebbero elaborare. IRIS e dcraw possono decomprimere un file raw in un formato dati come FITS, PGM o TIFF. IRIS o applicazioni simili possono eseguire gli algoritmi di riduzione del rumore necessari sui dati grezzi estratti. Il collegamento mancante nella catena di elaborazione è una semplice applicazione che prende come input l'immagine grezza elaborata e il file raw originale (di fondamentale importanza per i metadati dell'immagine che contiene, che sono in gran parte o interamente rimossi dalle applicazioni che sono in grado di fare il NR), quindi inserire l'immagine elaborata al posto dell'immagine non elaborata e scrivere l'output in un formato raw standard (ad esempio, un file DNG non elaborato). Quindi qualsiasi convertitore raw che comprende il formato raw standard può elaborare il risultato e l'utente può utilizzare il flusso di lavoro standard da quel momento in poi. Le conseguenze del rumore Rumore, gamma dinamica e profondità di bit Sia Canon che Nikon hanno introdotto un livello di quantizzazione più fine del segnale per digitalizzare e registrare i dati grezzi al sensore, passando dalla profondità tonale a 12 bit nei modelli più datati alla profondità tonale a 14 bit (e superiore) nei modelli più recenti. A priori, ci si potrebbe aspettare che questa transizione porti a un miglioramento della qualità dell'immagine in quanto i dati a 14 bit non hanno oltre quattro volte i livelli (16384) rispetto ai dati a 12 bit (4096). Peccato che così non è: le aspettative sono insoddisfatte e il colpevole è il rumore . In assenza di rumore, la quantizzazione di un segnale analogico introduce un errore, poiché i valori analogici sono arrotondati a un valore “digitalizzato” nell'ADC. Nelle immagini, questo errore di quantizzazione può causare la cosiddetta posterizzazione, in quanto i valori dei pixel vicini sono tutti arrotondati allo stesso valore digitalizzato. Un esempio è mostrato nella figura seguente, dove in Photoshop è stata generata, usando lo strumento “sfumatura”, un'immagine in scala di grigi a 8 bit con un gradiente tonale uniforme. La profondità di bit è stata quindi troncata a cinque bit (32 livelli tonali invece di 256) utilizzando due regolazioni successive al fine di limitare l'intervallo di output a 0-31 partendo da intervallo di input di 0-255. La differenza è evidente. Queste due regolazioni successive comprimono prima l'intervallo tonale, (troncando i tre bit più bassi), quindi il livello di regolazione del secondo livello ripristina l'intervallo del gradiente dal nero al bianco sul monitor. L'istogramma dei gradienti a 8 e 5 bit viene modificato di conseguenza, e lo si può vedere nell’immagine seguente Considerate ora l'effetto del rumore sulle transizioni tonali. Il rumore equivale a salti casuali di tonalità tra pixel vicini: più grande è il rumore, più grandi sono i salti casuali. Se i salti sono più grandi dell'intervallo tra i successivi valori quantizzati della tonalità, gli effetti di posterizzazione saranno resi impercettibili dal. Il livellamento delle transizioni attraverso l'effetto del rumore, sacrificando la risoluzione spaziale per una transizione regolae ma rumorosa, è noto come dithering . La Figura successiva mostra cosa succede quando il rumore della deviazione standard a 12 livelli viene aggiunto al gradiente tonale prima del del troncamento (dei bit) alla profondità tonale a 5 bit (dove il più piccolo salto consentito nella tonalità è di 8 livelli nella scala 0-255). Il rumore è più che sufficiente per eliminare ogni traccia di posterizzazione. La posterizzazione può verificarsi in presenza di rumore, ma solo quando la fase di quantizzazione è sostanzialmente più grande del rumore stesso. La Figura successiva mostra l'effetto della diminuzione della profondità di bit sul gradiente rumoroso, fino a quando il rumore è sostanzialmente più piccolo della dimensione del gradino. La posterizzazione diventa evidente quando la fase di quantizzazione supera sufficientemente la larghezza del rumore, i salti casuali nella tonalità dovuti al rumore non sono più in grado di “compensare” i salti discreti dovuti alla quantizzazione. È importante che il rumore sia presente prima della quantizzazione dei livelli (come avviene nell'elaborazione del segnale dal sensore della fotocamera, dove il rumore è fornito dall'elettronica del sensore e dalla statistica dei fotoni), prima che il segnale raggiunga il convertitore analogico digitale. Gestire le transizioni tonali tonali attraverso l'aggiunta di rumore dopo la quantizzazione è molto meno efficace, con un risultato ben diveso da quanto mostrato, appunto, nella figura di cui sopra.. La quantizzazione del segnale dal sensore in step molto più fini rispetto al livello del rumore è quindi superflua e dispendiosa. Quantizzare il rumore in gradini molto più grandi rispetto al livello del rumore rischia di far posterizzare l’immagine (ricordate che finché il rumore supera la fase di quantizzazione, la differenza tra una quantizzazione grossolana ed una fine è pressoché impercettibile). Idealmente, il rumore dovrebbe superare leggermente il passo di quantizzazione, in modo che gli errori di arrotondamento introdotti dalla quantizzazione stessa siano trascurabili e che non vengano sprecati bit nella digitalizzazione del rumore. Ricordo che i dati grezzi non sono mai posterizzati. Ciò non significa, tuttavia, che la posterizzazione non possa sorgere tra la conversione non elaborata e la post-elaborazione: la condizione per l'assenza di posterizzazione è che il rumore superi sempre la fase di quantizzazione. Abbiamo visto che la compressione dei livelli e il bit truncation possono reintrodurre la posterizzazione (nella figura di sopra, a causa della compressione dei livelli, la posterizzazione è sempre più evidente man mano che si riduce il numero di bit. A 2 bit è particolarmente evidente, nonostante il rumore). Le regolazioni dei livelli / curve e la correzione della gamma comportano la compressione dei livelli in alcune parti dell'istogramma, realizzando di conseguenza un troncamento dei livelli in alcune zone del’immagine. Il ricampionamento comporta la modifica dei valorei dei pixel adiacenti (viene fatta la media), cosa che può ridurre il livello di rumore al di sotto della fase di quantizzazione: questo come conseguenza può introdurre la posterizzazione laddove prima non esisteva. Quando si verifica la posterizzazione, è necessario riconsiderare la catena di elaborazione che l'ha prodotta e cercare di trovare un percorso alternativo che la eviti. Il punto principale da ricordare è che la profondità di bit dei dati grezzi non è mai il colpevole di questo problema. Facciamo un esempio per rendere meglio l’idea. Supponiamo, al fine di spiegare come la post-elaborazione può annullare l'effetto di dithering del rumore, di applicare un filtro mediano di raggio 5 sulla scala tonale troncata a 5 bit: Il filtro mediano sembra progettato appositamente per introdurre la posterizzazione. In una lista ordinata di numeri, la mediana è il numero medio della lista (o la media dei due numeri centrali se la lista è di lunghezza pari). Ad esempio, la mediana dell'elenco {4,8,8,12,16} è 8. Nell'elaborazione delle immagini, il filtro mediano sostituisce il valore di un determinato pixel con la mediana di tutti i pixel all'interno del raggio scelto di quel pixel. In un’immagine con il gradiente troncato (comprensivo di rumore), le fluttuazioni del rumore ingannano l'occhio facendogli “vedere” valori intermedi alle tonalità grazie alla presenza di una percentuale di pixel aventi i valori quantizzati vicini. In pratica, il nostro occhio, “approssima” le differenti zone dell’immagine (piccole zone). Spostandoci di quale pixel, l’occhio effettua lo stesso lavoro ed ovviamente il valore “letto” è differente in quanto è differente l’insieme dei pixel preso in considerazione. A differenza dell’occhio, però, il filtro mediano applica lo stesso valore ad una quantità ben definita di pixel. L’occhio a questo punto non può più mediare valori differenti ma “media” lo stesso valore, ovvero vede la posterizzazione. Il filtraggio mediano è un filtro molto semplice e anche molto comune e viene utilizzato in alcuni algoritmi di conversione grezzi (ad esempio, il convertitore raw gratuito dcraw) perché rimuove gli effetti dei pixel caldi e dei valori anomali estremi nella distribuzione del rumore, pixel estremamente visibili all’occhio umano (tipo i pixel rossi quando si fotgrafa il nero) . Quindi il filtro mediano filtra effettivamente il rumore, ma allo stesso tempo introduce la posterizzazione. Esistono comunque algoritmi più sofisticati che possono filtrare il rumore senza introdurre la posterizzazione. Nota: il troncamento dei bit non comporta alcuna modifica sui dettagli (sempre in presenza di rumore). Per rendere l’idea guardate la foto seguente. La transizione da 8 a 6 bit ha praticamente apportato zero cambiamenti all’immagine, rimasta quasi identica. Riassumendo il concetto: uno dei principali miglioramenti dichiarati della profondità tonale a 14 bit era quello di consentire transizioni tonali più uniformi, ma la maggiore profondità di bit non aiuta in presenza di rumore. Curiosamente, la maggior parte delle fotocamere a 14 bit sul mercato, soprattutto quelle della prima generazione come la Nikon D300 o la Canon 1D3 non merita la registrazione a 14 bit. Il rumore è più alto di quattro livelli nello scatto a 14 bit. I due bit aggiuntivi sono casualmente fluttuanti, poiché i livelli sono fluttuanti casualmente di +/- quattro livelli o più. Dodici bit sono invece adeguati per registrare i dati dell'immagine senza alcuna perdita di qualità nella stessa. Fuji, al contrario di Canon e Nikon, nella sua prima serie di fotocamere riuscì a risolvere il “problema”: ci sono due serie di pixel di diversa sensibilità sui sensori. Ogni tipo di pixel ha meno di 12 bit di intervallo dinamico, ma l'intervallo totale esteso dall'estremità superiore del pixel meno sensibile all'estremità inferiore del pixel più sensibile è più di 13 stop e pertanto la registrazione a 14 bit è garantita, e di qualità. Andando ad analizzare nel dettaglio il modo di registrazione della Nikon (per esempio nella D300), questa è sostanzialmente differente tra 12 e 14 bit. In particolare, il frame rate quando si registra a 14 bit rallenta di un fattore 3-4. La lettura del sensore è più “lenta” il che consente di leggere la luce in modo più accurato, per cui è possibile che si verifichi un miglioramento sensibile (ma ideale) nelle immagini a 14 bit rispetto a quelle 12 bit (in particolare, minore rumore di lettura, incluso il rumore del pattern). Ciò non significa, tuttavia, che i dati debbano essere registrati con una profondità tonale di 14 bit: il miglioramento della qualità dell'immagine deriva dalla lettura più lenta. Miglioramento che viene annullata dal fatto che il rumore è ancora oltre i quattro livelli a 14 bit. Il che fa si che l'immagine finale registrata a 12 bit è comparabile con quella a 14 bit in quanto presenta meno rumore. S/N e esposizione Una massima comune nella fotografia digitale è che la qualità dell'immagine è massimizzata "esponendo a destra" (ETTR) - cioè aumentando l'esposizione il più possibile senza tagliare i punti salienti. Spesso si afferma che, nel fare ciò, si fa il miglior uso del "numero di livelli disponibili" nei dati grezzi. Il motivo per cui si pensa in questo modo è che, poiché raw è un mezzo di acquisizione lineare, ogni stop in più che si usa nell'esposizione permette di accedere al bit successivo più alto nei dati digitali e al doppio dei livelli grezzi utilizzati nella cattura del file raw. Ad esempio, in un file a 12 bit, il limite massimo di esposizione ha 2048 livelli, il successivo livello più alto ha 1024 livelli, quello inferiore ha 512 livelli e così via. Sembrerebbe ovvio che i dati dell'immagine di più alta qualità deriverebbero dalla concentrazione dell'istogramma dell'immagine nelle zone di esposizione più elevata (quindi a destra), dove l'abbondanza di livelli consente transizioni tonali più fini. Tuttavia, il problema non è il numero di livelli non elaborati in un dato segmento di dati grezzi: il punto è che esponendo a destra, si ha un rapporto segnale/ rumore più alto. Crescendo il rumore, molti livelli grezzi disponibili nelle zone di esposizione più elevate sono ampiamente sprecati nel digitalizzare il rumore, come spiegato nelle lezioni precedenti (il parallelo tra 12 e 14 bit). Va vcomunque detto che, nelle fotocamere di ultima generazione, la gestione del rumore è molto migliorata e l’incremento di S/R è molto più limitata: ciò significa che con i top di gamma esporre a destra ha senso, a differenza delle fotocamere più datate o non al top dove, al contrario, non ha del tutto senso. Facciamo un esempio. Supponiamo di scattare una foto esposta a destra a ISO 3200. Quindi catturamo la stessa immagine con la stessa velocità dell'otturatore e la stessa apertura ma a ISO 1600. Quest'ultima immagine sarà sottoesposta secondo la tecnica ETTR. In particolare, l'idea che il beneficio dell'ETTR derivi dal "numero di livelli disponibili" suggerisce che la qualità dell'immagine sarebbe peggiore a ISO 1600 rispetto a quella a ISO 3200, poiché essendo uno stop più in basso e quindi essendo l’istogramma non tutto a destra, si utilizzano solo la metà dei livelli disponibili. Tuttavia, come abbiamo visto, il rumore è molto più alto di due livelli in tutte le zone di esposizione a ISO 3200, il che significa che i livelli aggiuntivi ottenuti scattando a ISO 3200 vanno semplicemente a digitalizzare il rumore e non sono quindi di alcun beneficio nel migliorare la qualità dell'immagine. Va comunque detto che le due immagini sono pressoché identiche in termini di qualità in quanto: Il rumore del fotogramma sarà lo stesso nei conteggi di fotoni per la stessa esposizione (diaframma e tempo di posa): il rumore del fotone è già presente nella luce prima che colpisca il sensore. Nei livelli grezzi, il rumore del fotone a ISO1600 sarà la metà di quello ISO3200 perché il guadagno (fotoni / livello grezzo) è il doppio. . Il rumore letto per ISO 1600 (13,4 livelli grezzi) è all'incirca la metà di ISO 3200 (26,2 livelli grezzi). In questo modo sia il rumore letto che il rumore di scatto saranno la metà in ADU per l'immagine ISO 1600 rispetto a ISO 3200. Ogni caratteristica dell'istogramma grezzo dell'immagine scattata a ISO 1600 si verifica a metà del valore grezzodell’immagine ISO 3200. Pertanto, l'istogramma grezzo relativo allo scatto a ISO 1600 e il rumore associato a ciascuna porzione di esso saranno la metà rispetto allo ascatto ISO 3200 con la stessa apertura / velocità dell'otturatore. Raddoppiando semplicemente tutti i valori grezzi dei pixel dello scatto ISO 1600 si otterrà un'immagine quasi identica allo scatto ISO 3200. Ciò non significa che esporre a destra è sbagliato, anzi. La giusta ragione per esporre a destra la si può vedere dalla figura di seguito Nel grafico è mostrato l'aumento del rapporto segnale-rumore con l'aumento dell'esposizione. Aumentando il numero di fotoni catturati, il rapporto S / N migliora e la qualità dell'immagine migliora in proporzione al rapporto S / N migliorato. Ad esempio, l’immagine scattata a ISO 1600 scattata sopra, ha un punto di luce in più rispetto al corrispondente scatto ISO 3200 e (supponendo che le condizioni di scatto lo consentano) aprendo il diaframma di un stop in più o rallentando la velocità dell'otturatore di metà, il rapporto S / N migliorerà (facendo ciò stiamo spostando l’istogramma a destra). Scattare a ISO sempre più bassi continua a fornire una quantità maggiori di informazioni nelle luci, e quindi è possibile un'esposizione più alta, consentendo di ottenere un rapporto S/N più alto. Il risultato finale è che l'esposizione a destra con il valore ISO più basso possibile fornisce la massima qualità dell'immagine. Ma questo significa che bisogna usare ISO bassi per avere la massima qualità? No. Usare ISO più alti è un vantaggio quanso si lavora nelle ombre piuttosto che nelle zone di massima luce dove "ci sono più livelli". Il grafico di sopra mostra come il rumore (misurato nei livelli grezzi) aumenta con l’aumento di ISO. Il rumore di lettura R , ricordo, è pari a R 2 = (GR 0 ) 2 + (R 1 ) 2 Quindi il rumore R è funzione di rumore R 0 proveniente dai componenti del circuito a monte dell'amplificatore ISO, del guadagno ISO pari a G e del rumore R 1 derivante dai componenti del circuito a valle dell'amplificatore ISO. Aumentare il guadagno ISO G enfatizza il contributo del rumore a monte, al punto che ad alti ISO il rumore letto è quasi interamente dovuto al rumore a monte R 0 , con un contributo trascurabile dai rumori a valle R 1 . Il rumore misurato nell'ADU è un rumore riferito all'uscita, ovvero è il rumore a valle dell’amplificazione. A volte è utile riportare il rumore al suo equivalente in ingresso, quello sui fotositi, in modo da confrontarlo con il rumore del fotone, entrambi misurati in fotoelettroni. Ciò si ottiene moltiplicando il fattore di conversione tra elettroni e ADU per il guadagno g = U / G . U è una costante (il cosiddetto guadagno universale ) e G è l'impostazione ISO. Per cui, la formula diviene: (R in elettroni) 2 = [g * (R in ADU)] 2 = U 2 (R 0 2 + R 1 2 / G 2 ) Ovvero il rumore di lettura diminusice con ISO considerato il “elettroni equivalenti”. Il motivo di questa diminuzione è l'influenza decrescente del rumore a valle R 1 sull’amplificazione. Questo viene diviso per il guadagno ISO, e quindi diventa più piccolo all’aumentare di ISO, mentre il rumore a monte, non amplificato, rimane costante In conclusione : il rumore di lettura agli alti ISO è molto più piccolo del rumore di lettura a ISO bassi, in termini di errore nel conteggio dei fotoni che rappresenta. Ciò significa che si ottiene una migliore qualità dell'immagine quando si usa un valore ISO più elevato per il quale il segnale non è troncato. 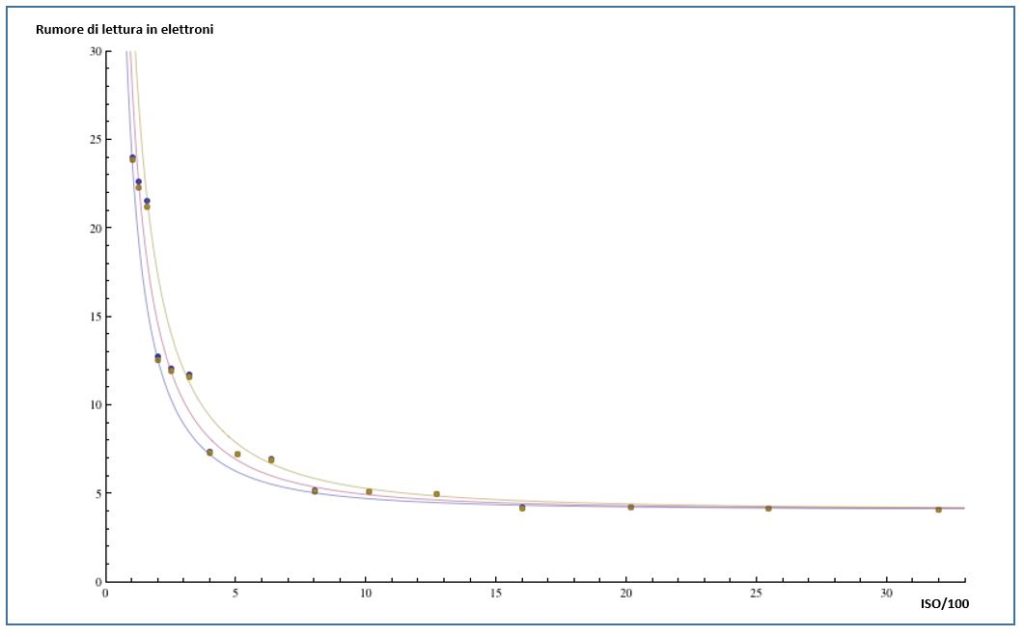Si vede chiaramente questa tendenza quando si traccia l'equivalente fotonico del rumore di lettura in funzione del valore ISO: L'effetto è piuttosto marcato: R 1 è oltre cinque volte più grande di R 0 , quindi quando il suo contributo diminuisce, il rumore residuo è oltre cinque volte più piccolo. Il rumore letto ad alti ISO si livella perché smette di ricevere contributi dall'elettronica a valle. D'altro canto, il contributo a valle è il più grande a valori ISO bassi. E non di poco. Al fine di tenere conto anche di questo fatto per decidere la corretta esposizione da utilizzare, è utile modificare la figura riportante il rapporto S/N rispetto ai valori ISO che abbiamo visto prima. 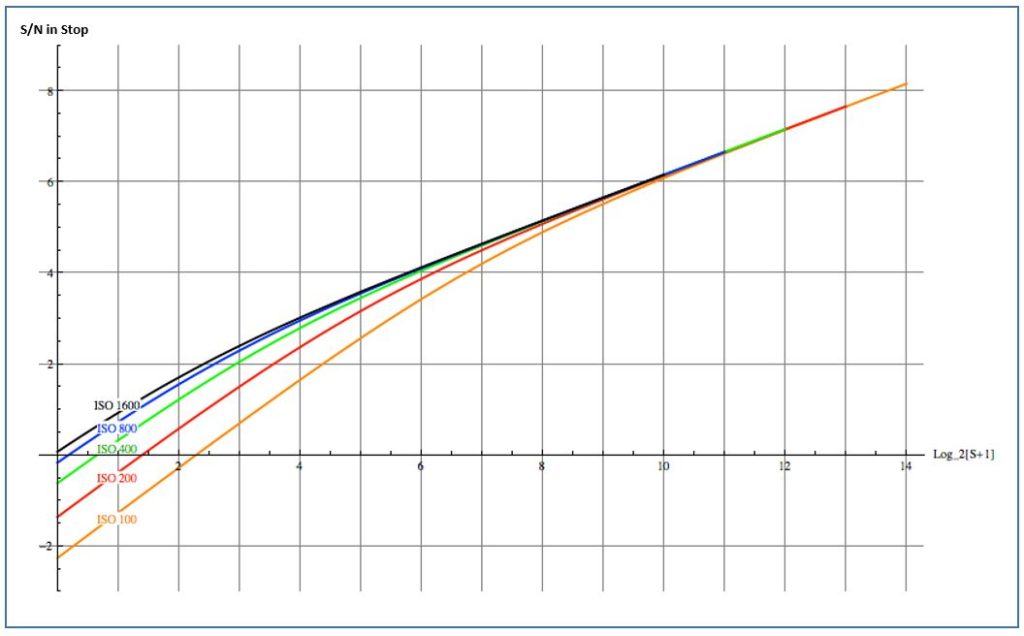La figura di seguito mostra i rapporti S/N in funzione del livello grezzo normalizzati alla stessa esposizione: Ci sono diversi modi per interpretare questo grafico. Se si ha la possibilità di abbassare ISO e tempo di posa (o allargare l'apertura), il S/N più alto per l'immagine si ottiene aumentando l'esposizione, spingendo l'estremità destra dell'istogramma fino al bordo superiore del gamma di esposizione sull'asse orizzontale (l’approccio ETTR). Abbassando l'ISO di uno stop si spinge l'estremità superiore dell'intervallo dinamico di uno stop verso destra, e spingendo l'istogramma verso destra cresce il rapporto S / N, il che permette una migliore qualità complessiva dell'immagine. Se, d'altra parte, non è possibile aumentare i tempi di esposizione o incrementare l’apertura (congelamento del movimento, profondità di campo, ecc.), allora ha senso alzare l'ISO al fine di spostare nuovamente l’istogramma verso destra. Fare ciò permette di avere un vantaggio quasi nullo nelle luci (a destra del grafico), in quanto (come si vede dal grafico) tutte le curve sono convergenti dopo il valore di 10. Tuttavia migliora la qualità dell'immagine nelle ombre in quanto aumenta il rapporto S / N (a sinistra nel grafico). Date un occhiata ai grafici, in particolare nella zona di sinistra: passando da ISO 100 a ISO 200 si ottiene un notevole miglioramento all'estremità inferiore dell'esposizione (al costo di una certa lperdita di dettaglio - il fatto che sull’asse Y è più in alto). Passare da ISO 800 a 1600 non fa molta differenza nelle ombre (lo scarto è minimo). Al di sopra di ISO 1600 non vi è alcun guadagno nelle ombre ma intanto siamo saliti parecchio sull’asse delle ordinate il che significa perdere dettaglio. In soldoni: non ha senso spingersi troppo con gli ISO, in quanto più si sale con il valore ISO, minore è il vantaggio in termini di S/N. Sparare ad ISO alti non ha senso in quanto non c'è alcun miglioramento nel rumore di lettura misurato negli elettroni con una conseguente riduzione di dettaglio nelle luci. È meglio sottoesporre a ISO 1600, poiché si ottengono gli stessi dettagli nelle ombre e più detagli nele luci In conclusione: zone ad alta esposizione e/o ISO elevati, dove il rumore dei fotoni e il rumore di lettura pre-amplificazione dominano il rumore, sono piuttosto insensibili al valore ISO che viene scelta. La sottoesposizione di uno stop e il raddoppio dei valori non elaborati in post-elaborazione (ovvero l'applicazione della compensazione dell'esposizione), producono la stessa qualità dell'immagine dell'esposizione "corretta" in queste condizioni. In zone di esposizione più basse a ISO bassi, dove il rumore di lettura post-amplificazione diventa importante, il rumore di lettura scende di un fattore leggermente inferiore a due (in elettroni) quando l'ISO raddoppia. In questa situazione, sottoesporre di uno stop e raddoppiare i valori grezzi in post-elaborazione permette di far ottenenre più rumore rispetto all'esposizione corretta, in particolare nelle ombre. Nota finale: la sottoesposizione a ISO più bassi è esattamente ciò che fanno le fotocamere Canon quando è attivata la funzione Highlight Tone Priority (HTP) o le fotocamere Nikon quando Active D-Lighting (ADL) è abilitato. Invece di utilizzare il guadagno ISO impostato dall'utente, la fotocamera utilizza un ISO più basso (ma espone con l'apertura e la velocità dell'otturatore indicate), sottoesponendo effettivamente l'immagine. Questo fornisce più dettagli nelle luci. Durante la post-elaborazione, i dati dell'immagine possono essere ripristinati alla corretta esposizione, preservando le luci con una curva di tonalità modificata in zone di esposizione più elevate. La compressione NEF "lossy" Il fatto che la quantizzazione di un livello più “fine” del rumore è superflua (in quanto il rumore cancella l’impatto percettivo di transizioni tonali brusche), significa che molti dei livelli usati per registrare zone più alte dell’esposizione non sono necessari e anzi dispendiosi: in queste zone il il rumore dei fotoni è molto più grande della spaziatura dei livelli nei mezzitoni e nelle luci, almeno su una reflex digitale di medio livello. In parole povere, se il numero medio di fotoni è 10000, ci saranno fluttuazioni da pixel a pixel pari a sqrt [10000] = 100 fotoni nel campione. Supponiamo che ogni aumento di uno nel livello grezzo corrisponda a contare altri dieci fotoni ( cioè il guadagno g = 10 fotoni / ADU ): il rumore per questo segnale è pari a 100/10=10 livelli grezzi. La codifica lineare del segnale grezzo spreca la maggior parte dei livelli grezzi, poiché il rumore è molto più grande della fase di quantizzazione. Nelle ombre la situazione è un po’ differente. Supponiamo che il nostro segnale medio sia di 100 fotoni: le fluttuazioni del fotone sono sqrt [100] = 10 fotoni, che si traducono in +/- un livello grezzo con un guadagno g = 10 . In questo caso nessuno dei livelli grezzi viene "sprecato" nella digitalizzazione del rumore. L’ideale sarebbe avere un algoritmo che possa ridurre la spaziatura dei livelli ad alti valori del segnale (sulle luci) mantenendolo intatto quella per il segnale basso (le ombre) e facendo in modo che la spaziatura tra i livelli sia mentenga sempre al di sotto del livello di rumore (per evitare la posterizzazione). La compressione "lossy" NEF di Nikon è quanto più si avvicina a questo concetto: questa utilizza una tabella che mappa i livelli grezzi 0-4095 (per i 12 bit grezzi) in valori compressi in modo tale che non ci sia compressione nelle ombre, ma un crescente diradamento dei livelli per le luci, in funzione della relazione che abbiam visto prima in radice quadrata tra rumore di scatto e segnale. Il valore grezzo digitalizzato non compresso viene arrotondato al valore più vicino nella tabella di NEF. La quantità di compressione aumenta quando il valore grezzo non compresso aumenta oltre una certa soglia, nello stesso modo in cui il rumore fotonico (di scatto) aumenta con il livello di illuminazione. [caption id="attachment_11394" align="aligncenter" width="674"] Struttura base della tabella per la compressione NEF di Nikon. L'asse orizzontale è il valore grezzo compresso NEF. L'asse verticale è il valore grezzo a 12 bit non compresso. I valori non corrispondenti che corrispondono a un valore compresso vengono arrotondati al valore compresso più vicino. La curva blu è una trama della tabella di compressione, la curva rossa è la parabola più adatta alla parte non lineare delal tabella di compressione. 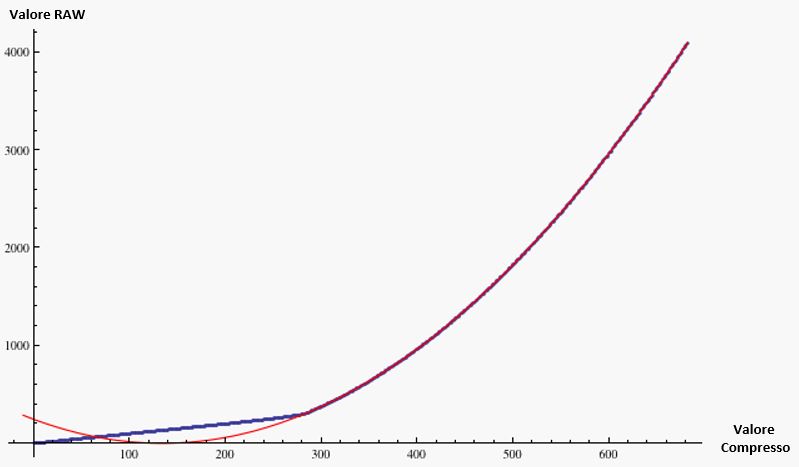[/caption] L'idea alla base della compressione NEF "lossy" è quindi quella di ridurre i livelli nelle luci in cui i livelli sono troppo finemente distribuiti rispetto alla rumorosità intrinseca della luce, ma mantenere la maggior parte o tutti i livelli nelle ombre in cui la magnitudo delle fluttuazioni del rumore è minore. Questo è il motivo per cui la tabella di compressione NEF è lineare all'estremità inferiore e quadratica più in alto. La parte quadratica è un riflesso della relazione quadratica tra rumore e segnale di luce (il rumore al quadrato è proporzionale al segnale): più alto è il segnale, più livelli possono essere ridotti. La parte lineare della tabella di compressione si attiva quando il segnale è sufficientemente basso da ridurre le oscillazioni del rumore, quindi non è possibile alcuna compressione senza perdita pesante di informazioni, ed il valore di uscita deve essere uguale al valore di input. Quantitativamente, il criterio appropriato è che un salto nel valore compresso C dovrebbe corrispondere ad un arco di valori grezzi S inferiore al rumore (che è almeno grande quanto il rumore di scatto pari a S/g ), in modo che il rumore continui a fare dithering sui salti più grandi dell’immagine compressa in cui sono stati eliminati i livelli. In altre parole, frac{dS}{sqrt{frac{S}{g}}}" align="absmiddle" /> Ed ecco la relazione tra i valori compressi e quelli grezzi dove C0 è un offset costante pari alla metà della lunghezza della parte lineare della tabella (dove la compressione non è possibile). La parabola più adatta alla parte non lineare della tabella di ricerca (ovvero la curva rossa nella figura di cui sopra), ha un valore di C0 = 134 e g = 18 . L’idea di fondo secondo cui i salti nei valori compressi non superano il rumore di scatto è che questo valore g dovrebbe essere maggiore del guadagno effettivo della fotocamera alla sua base ISO. In effetti, il tipico guadagno ISO di base per i modelli Nikon che utilizzano questa particolare tabella di compressione è pari a circa 6-8, quindi la condizione è soddisfatta con un buon margine di sicurezza. Per riassumere: Il modulo "lossy" di compressione NEF è un uso intelligente della teoria dell'informazione per risparmiare spazio eliminando livelli ridondanti. Il rumore che è inevitabilmente presente nelle luci ci permette di effettuare de facto una compressione è lossless , cosa che si ottiene anche con la “non” compressione negl scuri. In effetti, una vera e propria perdita di informazioni non c’è...se non ci si riferisce a ciò che è perso comunque a causa del rumore Pixel Grandi vs Pixel Piccoli Come confrontare rumore e gamma dinamica Le statistiche del rumore e della gamma dinamica sono genericamente tabellati per ogni tipo di fotocamera e si basano su misurazioni per i singoli pixel (sono direttamente i produttori a calcolare i valori). Ciò che invece non è creato di default è il paragone tra differenti fotocamere, soprattutto quando la dimensione dei fotodiodi, o più semplicemente pixel, è different Cominciamo con il dire che, in generale, pixel più piccoli sono più rumorosi. Perché? Supponete di unire un blocco da 2x2 di pixel in un "superpixel" grande, appunto, il doppio di un pixel di partenza. Il valore grezzo è proporzionale al numero di fotoni raccolti: combinando pixel, i conteggi dei si incrementa, diventando: S = S 1 + S 2 + S 3 + S 4 I rumori, come abbiamo visto in precedneza, si combinano in quadratura: N = sqrt [(N 1 ) 2 + (N 2 ) 2 + (N 3 ) 2 + (N 4 ) 2 ] Se i valori grezzi e i rispettivi contributi di rumore sono approssimativamente uguali, il segnale aggregato è quattro volte quello del singolo pixel, mentre il rumore complessivo è circa due volte il rumore del singolo pixel. Così il "superpixel" di quattro pixel ha due volte il rapporto S/N di qualsiasi dei suoi pixel che lo compongono. L'effetto di combinare pixel diventa più complicato nelle regioni in cui l'immagine contiene trame o dettaglii, dal momento che le fluttuazioni di rumore N i vengono mediati insieme alle variazioni tonali dei valori del segnale S i . La variazione locale del valore misurato dei pixel è composto in parte dal rumore, e quindi la riduzione quantitativa della variazione dei valori dei pixel non darà direttamente la quantità di rumore eliminato, così come la diminuzione della deviazione standard dei valori dei pixel relativi al valore medio del segnale farà, in generale, attenuare il segnale di un fattore due. Per riassumere: Al costo di avere metà della risoluzione lineare, il superpixel realizzato con l’aggregazione di un blocco 2x2 di pixel permette di ottenere fino a due volte il rapporto segnale-rumore. Ma questo rapporto S / N non esisteva già prima di iniziare a mettere insieme i pixel? Ovviamente si. Tutto ciò che abbiamo fatto combinando i pixel è stato quello di riddurre la risoluzione. Il punto è che il rumore e il rapporto segnale/rumore dipendono dalla scala spaziale sulla quale vengono misurati. In genere, S/N sarà due volte più grande al doppio della scala spaziale, come dimostra l'esempio della combinazione di pixel. Quindi, il rumore diminuisce in proporzione inversa alla risoluzione. Se si esegue il downsampling di un'immagine correttamente, si diminuisce la risoluzione ed il rumore diminuisce in proporzione alla variazione lineare della dimensione dell'immagine nelle regioni di tonalità uniforme (Questo perché l'effetto di sottocampionamento diventa più complicato nelle regioni in cui l'immagine contiene trama o dettaglio, dal momento che le fluttuazioni di rumore nei valori dei pixel vengono mediati assieme alla variazione tonale dell’esposizione). La conclusione è che il rumore è “risoluzione dipendente”. Se si confrontano due fotocamere aventi la stessa dimensione del sensore e pari tecnologie ma diverse risoluzioni (densità di pixel), quello con la più bassa risoluzione (densità di pixel inferiore) avrà meno rumore a livello di pixel. Lo stesso ragionamento vale quando si confrontano due modelli di fotocamere diversi con differenti dimensioni di pixel. A parità di altre condizioni (la percentuale di area di pixel attivi nella fase di raccolta della luce, l'efficienza dei pixel, ecc ) il numero di fotoni raccolti sarà proporzionale all'area del pixel, mentre il rumore di scatto (o dei fotoni) si scala in proporzione alla spaziatura dei pixel. Ad esempio, la Canon 40D ha 5,7 micron pixel, il suo guadagno (il numero di fotoni raccolti per livelli grezzo) è 3,1 per 14-bit ADU e ISO 400. Il numero di elettroni raccolti per livello grezzo per quadrato micron è pari a 3,1/5,7^2 = .095. La Canon 1D3, d'altra parte, ha 7,2 micron pixel e un guadagno di 5,0 per 14-bit ADU e ISO 400. L'efficienza luminosa di raccolta per unità di superficie è 0,097,sostanzialmente lo stesso della Canon 40D. Utilizzando la stessa tecnologia, Canon ha quindi raggiunto la stessa efficienza di raccolta della luce per unità di area del sensore per entrambe le telecamere. Di conseguenza, il rumore in fase di scatto in scala spaziale fissa è lo stesso per entrambe le telecamere. L’efficienza di raccolta della luce si traduce in fotoni, il numero dei fotoni determina il rumore in fase di scatto e ques’ultimo è la sorgente di rumore dominante nelle luci. Volendo fare un resoconto delle efficienze di raccolta di una serie di sensori, possiamo fare riferimento alla tabella di seguito dove sono riportate le efficienze di un po’ di sensori, marcati Nikon o Canon: 10D 1D2 D200 5D 350D 20D 400D D300 40D 1D3 50D D3 .042 .049 0,054 0,061 .064 0,076 0,083 0,089 0,095 0,098 .100 .113 capacità di raccolta della luce per unità di superficie dei sensori di vari modelli di fotocamere, tutte allo stesso ISO (e tutte a 12 bit). I dati relativi alla raccolta della luce per area unitaria nella precedente tabella si riferiscono all'efficienza del sensore ad una scala spaziale fissa anziché a a livello di pixel, al fine di rendere “innocua” la differenza di dimensione dei pixel delle varie fotocamere. L’uso della scala spaziale fissa è la metrica appropriata per confrontare diverse densità di pixel se si cattura la stessa immagine con due fotocamere con diverse densità di pixel, alla stessa lunghezza focale. Facendo il crop della stessa area su ogni immagine scattata da tutte le differenti fotocamere e ricampionando l'immagine alle stesse dimensioni, ci ritroveremmo con lo stesso rumore di scatto. Quindi, da quanto abbiamo detto, il rumore di scatto in scala spaziale fissa è indipendente dalla dimensione dei pixel per una data efficienza di raccolta. Per quanto riguarda l’altro rumore ”importante”, ovvero il rumore di lettura, affinché questi in scala spaziale fissa sia indipendente dalle dimensioni dei pixel, deve diminuire proporzionalmente alla spaziatura pixel: se la spaziatura dei pixel fosse dimezzata, ci ritroveremmo con quattro pixel (di dimensione pari alla metà) nell'area precedentemente occupata da uno solo, con un rumore di lettura relativo aggregato pari al doppio di quello dei nuovi pixel, dato che rumori combinano in quadratura). Pertanto, nuovi pixel devono avere metà rumore di lettura in modo che il rumore di lettura totale sia lo stesso di quello del pixel originale. E’ ciò possibile. Dipende. Il rumore di lettura varia con il variare di ISO, come abbiamo visto in precedenza. Questo significa che le cose potrebbero essere differenti ai vari ISO e non sempre potremmo ottenere ciò che vogliamo. Prendiamo per esempio la Canon 40D e la 1D3. A ISO 100, la 1D3 ha un rumore di lettura pari a 4,8 ADU, mentre la 40D ha un rumore di lettura di 5,5 ADU. A 1600 ISO, il rumore di lettura è 13,4 ADU per la 1D3 e di 22,6 ADU per la 40D. Va ricordato che i valori di rumore letti hanno “significati” diversi per le diverse fotocamere grazie alle loro differenti efficienze e alle differenti dimensioni dei pixel che comportano diversi livelli di risoluzione e conseguentemente diverse quantità di rumore osservato in un singolo pixel. Quindi si pone la questione di come questi numeri devono essere confrontati. Un modo per normalizzarli è confrontarli rispetto al rumore di scatto, convertendo i valori di rumore di lettura da ADU ai loro equivalenti fotoelettroni. Per convertire il rumore di lettura da ADU agli equivalenti in fotoelettroni, si deve moltiplicar il valore per il guadagno in elettroni/ADU. Ad esempio, il guadagno della 40D è di 3,1 elettroni / 14 bit ADU a ISO 100, mentre il guadagno della 1D3 è 5,0 elettroni / 14 bit ADU allo stesso ISO 100 (a ISO 1600, per la cronaca, i numeri ottenuti vanno divisi per 16, dato che il valore di guadagno è inversamente proporzionale a ISO). In termini di rumore di lettura, abbiamo questi valori: a ISO 100 17 elettroni per la 40D e 24 elettroni per la 1D3; a ISO 1600 4,4 elettroni per la 40D e 4.2 elettroni per la 1D3. Una seconda correzione deve essere fatta per compensare le dimensioni di pixel differenti. Per normalizzare il rumore di pixel di dimensioni differenti si dovrebbe riscalare in funzione dellas paziatura tra i pixel, in modo che si possa fare riferimento, alla fine, alla stessa scala spaziale. Quando si misura il rumore in elettroni, questa normalizzazione divide il rumore di lettura per la spaziatura dei pixel (pixel più grandi significa meno pixel per unità di superficie). Così a ISO 100, abbiamo17 / 5,7 = 3,0 per la 40D, 24 / 7,2 = 3,3 per la 1D3. A ISO 1600, si ha 4,4 / 5,7 = 0,77 per la 40D e 4,2 / 7,2 = 0,58 per la 1D3. Quindi, i pixel più piccoli fano meglio di quelli più grandi a basso ISO, mentre i pixel più grandi fanno meglio di quelli più piccoli ad alta ISO. I risultati di sopra potrebbero suggerire un leggero vantaggio in termini di gamma dinamica per i pixel piccoli a ISO bassi, rispetto a un leggero vantaggio per i grandi pixel ad alti ISO. D'altra parte, per i pixel minuscoli nelle fotocamere digitali “point&shot”, il rumore di lettura degli elettroni è praticamente indipendente dagli ISO. Inoltre, l'efficienza della raccolta della luce tende a essere ampiamente indipendente dalle dimensioni dei pixel su una gamma molto ampia di pixel, dai più grandi pixel delle DSLR fino ai più piccoli pixel delle “point & shot”. Quindi la gamma dinamica per area, che è la capacità massima di raccolta della luce per area divisa per il rumore letto per area, è in gran parte determinata dal rumore letto per area per il quale il confronto è peggiore per DSLR a ISO bassi e migliore per DSLR a alto ISO. Il fattore che limita il rendimento delle DSLR a bassi ISO risulta essere dovuto alla limitata gamma dinamica dell'amplificatore ISO e componenti ADC a valle del sensore, e non per colpa del sensore stesso (problema risolto per esempio con le ultime DSLR). Per confrontare pixel su una data area di un sensore, le normalizzazioni sopra riportate sono quelli appropriate. Tuttavia, spesso si ha l’interesse di confrontare il rumore complessivo dell'immagine provenienti da diverse dimensioni di sensori. Per ottenere questo risultato, serve un’altra metrica, così come un differente approccio. Per esempio, per confrontare due macchine come la 1D3 e la 40D, è necessario scattare a differenti lunghezze focali in modo che il campo visivo venga mantenuto fisso (rispettivamente 130mm e 160mm per i due modelli di cui sopra). Nel caso della stessa inquadratura, dovremmo riferire le caratteristiche di rumore non ad una scala spaziale fissa in micron, ma piuttosto ad una percentuale fissa della altezza del telaio. Un metodo adeguato per farlo è quello di dividere i valori di rumore per pixel per l'altezza del telaio in pixel (questo perché il rumore si combina linearmente nel numero di pixel combinati). Questa regola – empirica - ci dice che i sensori dalle dimensioni più grandi sono meno rumorosi dei sensori dalle dimensioni più piccole. Un semplice esempio è nuovamente ottenibile comparando la 40D rispetto alla 1D3; entrambi sono fotocamere da 10 MP, con 2592 pixel in altezza. Il rumore riferito alla fimensione del telaio è quindi lo stesso pe i due modelli e sono anche inferiori (misurata in ADU) a tutti i livelli di esposizione e valori ISO per la 1D3. I rumori di lettura sono simili (in unità foto-elettroni), ma i fotositi più grandi della 1D3 permettono di catturare più fotoni, il che fa salire il rapporto S/N. Sensori più grandi hanno elevati rapporti segnale / rumore, perché i sensori più grandi raccolgono più fotoni. Nota finale: Molto interessante è notare che, in funzione di quanto detto, le fotocamere poit & shot possono in qualche caso “superare” le sorelle maggiori (le reflex). Un esempio è dato dalla Panasonic FZ50, una superzoom da 10 Mpx con funzionalità RAW. Considerando il metodo descritto nelle precedenti lezioni per il rumore vs. Esposizione, si ottiene un guadagno g di circa .29 fotoni / 12-bit ADU a ISO 400. Dividendo per il quadrato dei 2 micron pixel si hanno .072 fotoni per ADU per micron quadrati. Valore che si colloca nel centro della tabella di cui sopra Tuttavia le calibrazioni ISO delle camere portatilisono diverse da quelle di una DSLR: la tipica lascia circa 3,5 stop tra il grigio medio e il valore raw di saturazione. Le poit & shot hanno una differenza di soli 0,5-1,0 top. Ciò significa che la taratura ISO di una Point & Shot è di circa 0,5-1,0 fermate in meno rispetto alla calibrazione ISO di una reflex, e quindi il valore di efficienza finale della FZ50 è più alto di 0,072 di un fattore 1,4-2,0, rendendo il sensore della FZ50 tra i più efficienti per unità di superficie nel catturare fotoni di qualsiasi altro sensore disponibile. Naturalmente il sensore è piccolissimo, solo 5,5 millimetri x 7,3 millimetri, quindi il rumore di scatto riferito alla dimensione del telaio è piuttosto scarsa, “bilanciando” in negativo il guadagno di cui sopra e facendo si che il sensore della Reflex sia, alla fine, vincitore. Ciò che si evince da questo calcolo è che un sensore di fotocamera digitale poit & shot può rivaleggiare o addirittura superare la performance delel DSLR in termini diefficienza di cattura dei fotoni e prestazioni di rumore di scatto. Ma che dire del rumore di lettura? Per la FZ50 si ha un rumore di lettura pari a 4,5 ADU ~ 5.4 elettroni. Quello della Canon 1D3 (normalizzato) è 1,2 12 bit ADU = 24 elettroni a ISO 100, e la spaziatura dei pixel è di 7,2 micron. Quindi il suo rumore di lettura è pari a 24 / 7,2 = 3,3. Il rumore di lettura della FZ50 ha un valore pari a 5,4 / 2,0 = 2,7. Quindi, ancora una volta, l'FZ50 è migliore della migliore reflex digitale in lettura agli ISO più bassi. Il confronto diventa ancora migliore se calcoliamo le differenze a differenti ISO: il rumore di lettura della 1D3 a ISO 1600 è 3,4 ADU a 12 bit = 4,2 elettroni, mentre la FZ50 sono ancora circa 5,4. Ora, quando dividiamo per la spaziatura dei pixel per riferirsi alla scala spaziale fissa, il confronto favorisce sostanzialmente la DSLR a pixel grandi, anche quando viene calcolata la relativa calibrazione ISO. Per riassumere: Tra le importanti misure di qualità dell'immagine ci sono il segnale-rumore del processo di cattura e risoluzione. Abbiamo dimostrato che per un sensore dal formato fisso (stesse caratteristiche), l'efficienza di raccolta della luce per unità di superficie è sostanzialmente indipendente dalla dimensione dei pixel , su una vasta gamma di dimensioni di pixel da 2 micron a oltre 8 micron, ed è quindi indipendente dal numero di megapixel. Le prestazioni di rumore per unità di superficie sono solo debolmente dipendenti dalla dimensione dei pixel. Il rapporto S/N per unità di superficie è molto simile per una vasta gamma di dimensioni di pixel. C'è un vantaggio a grossi pixel e nelle ombre (alti ISO), dove il rumore di lettura è un importante fattore di penalizzazione della qualità dell'immagine, e i grandi pixel attualmente hanno un minore rumore di lettura rispetto ai pixel piccoli. Al contrario, per le luci (bassi ISO), la situazione è invertita: pixel più piccoli performano un po' meglio in termini di rapporto S / N (offrendo una risoluzione maggiore). L'altra principale misura della qualità dell’immagine è la risoluzione in funzione dell’altezza dell’immagine: essa è per definizione indipendente dalla dimensione del sensore, e dipende solo dal conteggio dei (mega)pixel. Più megapixel, più risoluzione, fino ai limiti imposti dalle ottiche del sistema. Realizzazione di un modello matematico (advanced) Il rumore di lettura La seguente equazione mostra il nostro attuale modello di sensore. Poiché il termine "EL", che rappresenta la quantità di elettroni raccolti dal fotosito, è una variabile casuale, la mostreremo utilizzando il carattere in grassetto. ADU = M ⋅ EL

Nei sensori APS (Active Pixel Sensor), ogni fotosito è collegato alla circuiteria elettronica incaricata di convertire la carica degli elettroni -prodotta dai fotone che colpiscono il sensore- in tensione, e di condurla come ingresso al convertitore A/D. Poiché questa linea di elaborazione non è perfetta, l'uscita del convertitore A/D non è esattamente proporzionale alla quantità di elettroni provenienti dagli scatti del fotone. C'è sempre una polarizzazione o un livello base di ADU che esce dal convertitore A/D, anche quando non ci sono elettroni nei siti fotografici, come in una foto scattata con il copriobiettivo inserito. Questo rumore è chiamato Read Noise (rumore di lettura) e in sintesi deriva dal processo di lettura di "quanti" elettroni sono nel fotosito e di "calcolo" del corrispondente valore di ADU.

La sequenza seguente mostra come come il segnale (B) viene miscelato con il rumore letto (A), e come anche dopo che il bias del rumore letto viene rimosso (da C a D) il segnale risultante (D) contiene ancora il rumore letto (C). Il rumore di lettura del sensore . È come "un segnale falso" intorno ad una media di 500 ADU (in questo esempio). L'intensità del rumore in questi grafici è rappresentata dall'altezza della banda evidenziata in verde. Il segnale raccolto nei fotositi . Anche quando la sorgente è illuminata uniformemente con un valore atteso di 300 ADU, il segnale (linea rossa sottile - B) non è piatto perché contiene il Rumore del Fotone. L'uscita del convertitore A/D , rappresentata dalla linea spessa rossa (C), contiene il rumore di lettura ed il segnale. La "correzione" del Rumore di Lettura . Il "segnale falso" di lettura del rumore viene sottratto dai valori ADU. Se il risultato di questa sottrazione è un valore negativo, il pixel viene azzerato. Ora il segnale rosso ha una media di 300 ADU come previsto, ma il rumore aggiuntivo che proveniva dal rumore di lettura è ancora lì: l'altezza della banda evidenziata in verde è la stessa del punto 3. Questa correzione del rumore di lettura , in alcune marche di fotocamere (ad esempio Nikon) è fatta in-camera o altrimenti da software di elaborazione delle immagini (in formato grezzo, raw). La stessa rappresentazione è riportata nel grafico di seguito, ma dal punto di vista dell'istogramma. Si nota immediatamente come l'istrogramma "originale" sia modificato in maniera sostanziale dal rumore di lettura. 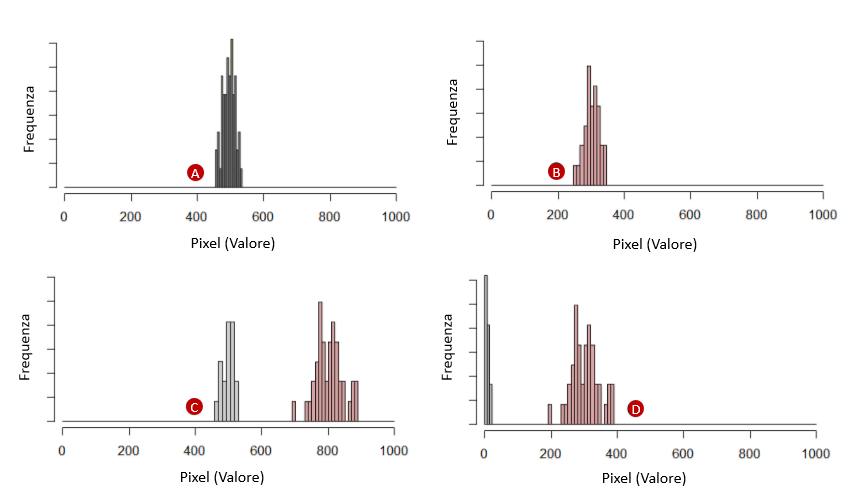Aggiungeremo ilRumore di lettura al nostro modello usando il termine "RNS", che rappresenta il rumore di lettura della "componente di segnale" in ogni lettura ADU del fotosito. È in grassetto perché è una variabile casuale, varia da un fotosito all'altro. ADU = M ⋅ EL + RNS

Per semplificare le nostre formule, il termine "RN" rappresenterà il Rumore di Lettura (Read Noise), mentre "RN²" rappresenterà la sua varianza: Var(RNS) = RN² StdDev(RNS) = RN Applicando l'operatore del valore atteso a entrambe le estremità dell'equazione sopra riportata, si ottiene: Eva(ADU) = M ⋅ Eva( EL ) + Eva ( RNS ) = M ⋅ λ + Eva( RNS ) = M ⋅ λ +μ RNS

La formula sopra riportata indica il valore medio del pixel, in un'immagine con rumore di lettura, viene incrementato del segnale medio di tale rumore di lettura. Tuttavia, come abbiamo già visto, questo errore sistematico viene rimosso nella "correzione del rumore di lettura". Rappresenteremo tale correzione nel nostro modello sottraendo il termine μRNS: ADU_RNC=M ⋅ EL + RNS - μ RNS

Eva(ADU RNC ) = M ⋅ λ + Eva ( RNS ) - μ RNS = M⋅λ + μ RNS - μ RNS = M⋅λ

Nella parte sinistra della prima equazione, il termine ADU sottoscritto con "RNC" rappresenta i valori ADU in un'immagine raw con il rumore di lettura corretto. Dopo la correzione del rumore di lettura, il segnale "falso"dovuto al rumore di lettura viene rimosso sottraendo la media dai valori ADU. In questo modo, come si può vedere nella seconda equazione, il valore atteso dell'immagine grezza "Con rumore di lettura corretto non ha il "segnale falso" di lettura. Si noti che l'RNS è una variabile casuale, ma il suo μRNS medio è una costante. Nota: Dobbiamo distinguere due diversi effetti del rumore di lettura: aggiunge un bias ai valori del fotosito aumenta la loro varianza. La correzione del rumore in lettura rimuove la distorsione nei valori dei siti foto, ma anche se la varianza aggiunta rimane nell'immagine. Questo è rappresentato nel primo gruppo di grafici più sopra, dove il rumore del segnale (B) viene incrementato dal rumore lettura(C) e rimane tale anche dopo la correzione del rumore di lettura stesso (C). Siamo interessati al rumore nel file immagine grezzo che elaboreremo per ottenere la nostra immagine finale, e che sarà l'immagine grezza dopo la correzione del rumore di lettura. Per questo motivo, d'ora in poi, continueremo ad utilizzare come modello, la formula con la lettura del rumore "segnale falso" rimosso. ADU RNC =M ⋅ EL + RNS - μ RNS

Deve essere chiaro che il Rumore di Lettura è completamente indipendente dal Rumore del Fotone. Il rumore di lettura è correlato alle imperfezioni dell'elettronica del sensore ed è indipendente dall'intensità della luce che colpisce il sensore. Al contrario, il Rumore del fotone (o fotonico) è causato dalla natura fisica della luce e dalla sua intensità, ma è totalmente estraneo al processo di elaborazione del sensore.

Questa indipendenza tra il Rumore di Lettura e il Rumore di Fotone significa che la Varianza della loro somma è uguale alla somma delle loro Varianze. Si ottiene la varianza nel modello che applica l'operatore della varianza ad entrambe le estremità dell'equazione sopra riportata. La varianza di una variabile non casuale come μRNS è pari a zero. Var(ADU) = Var (M ⋅ EL ) + Var( RNS ) + Var (μ RNS ) = M²⋅λ + RN²

Ora possiamo inserire SNR nel nostro modello attuale. Ricordate che il rumore è la radice quadrata della varianza, che è la deviazione standard. Se confrontiamo l'SNR di questo modello di sensore, su cui abbiamo sia il rumore di scatto che rumore di lettura con il sensore ideale, otteniamo il comportamento mostrato nel grafico seguente. Notare come il rumore di lettura fa male alle parti più scure dell'immagine diminuendo il SNR. Per una maggiore luminosità, l'effetto del rumore di lettura svanisce e l'SNR si avvicina asintoticamente al sensore SNR ideale. Si dice che il rumore di lettura imponga un limite inferiore al campo del sensore (vedremo dopo perché). Supponiamo, per semplicità di calcolo, che non tollereremo un SNR inferiore a 2. Nel sensore ideale (linea tratteggiata), ciò richiederebbe esposizioni che portano i valori di luminosità al di sopra o uguale a 4 ADU. Tuttavia, nel sensore con rumore di lettura, questo richiede esposizioni con valori di ADU superiori o uguali a 8 ADU, ovverosia saremo costretti ad utilizzare 1 stop in più. Ciò significa che il rumore di lettura ha ridotto la gamma dinamica della telecamera di 1 stop: per evitare livelli di rumore non tollerati non è possibile utilizzare un ulteriore stop. In alcune marche di fotocamere, un'esposizione con il tempo di posa più veloce possibile e il paraluce davanti all'obiettivo, permette di ottenere un'immagine grezza con solo il rumore di lettura (chiamato "cornice nera"), corrispondente alla fase C dei grafici precedenti. In questo caso l'elaborazione dell'immagine grezza deve rimuovere il rumore di lettura. Le fotocamere Nikon offrono immagini raw con il rumore di lettura già corretto, corrispondente alla fase D dei grafici di prima. In questo caso, i valori dell'immagine grezza sono rappresentati dalla formula dell'ultimo modello. Nel caso delle fotocamere Canon, il software di elaborazione delle immagini deve eseguire la correzione rumore di lettura. La maggior parte delle fotocamere Nikon include, nel file immagine grezzo, dati provenienti dall'area del sensore contenente i fotositi "Optical Black" (OBN). Questi fotositi hanno uno scudo scuro che li copre, in modo che la luce non può colpire loro. Sono utili per scoprire il livello del segnale del rumore di lettura. 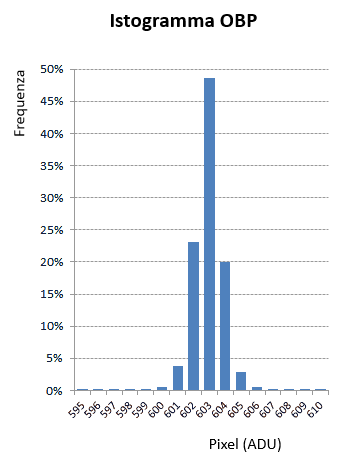Il sensore utilizza questi dati per effettuare la "correzione del rumore di lettura" in-camera. L'istogramma sopra riportato corrisponde ai dati reali dei pixel nell'area OS in un file immagine grezzo da una fotocamera Nikon D7000 utilizzando ISO 100. Ciò corrisponde all'istogramma nella fase A dei grafici di prima. Nel profilo istogramma, il 96% dei pixel ha un valore uguale o inferiore a 604 ADU. Possiamo ottenere un indizio su come questo valore viene utilizzato per la "correzione del rumore di lettura" in-camera osservando i valori superiori nell'istogramma di un'immagine fortemente sovraesposta, come nell'immagine seguente. 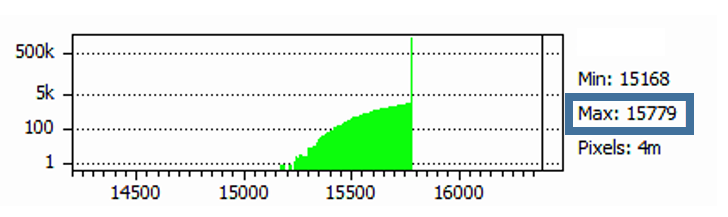L'istogramma sopra riportato corrisponde ai dati grezzi reali di un'immagine sovraesposta scattata con una Nikon D7000 utilizzando anche ISO 100. Notare come i pixel verdi che traboccano i 16.383 ADU, pari al limite superiore nei file raw a 14 bit, sono stati taglilati a quel valore massimo nella fase C (sempre nei grafici di sopra). Nella fase D, il valore 604 ADU -selezionato tra i pixel OB- è stato utilizzato dal sensore per "correggere il rumore di lettura" dell'immagine, risultando in 16.383 - 604 = 15.779 ADU, che è il valore massimo che vediamo nell'istogramma finale di cui sopra. Dopo questa correzione, solo il 4% = 100% - 96% del "segnale" di lettura del rumore rimane ancora nei valori dell'immagine. Ma oltre ad essere una bassa percentuale, sono -alla maggior parte- valori di circa 7 ADU (i restanti valori di Read Noise rispetto al 604 sottratto) aggiunto all'immagine. Il rumore di PRNU Non tutti i fotositi sono uguali (anche quelli che filtrano la luce delo stesso colore), o meglio non sono ugualmente sensibili alla luce. Le micro-lenti di ogni fotosito, lo strato che raccoglie gli elettroni prodotti, il convertitore A/D e gli altri elementi della circuiteria dei sensori non sono tutti prodotti uguali l'uno all'altro. In altre parole, il termine "M" nel nostro modello, non è esattamente lo stesso valore per ogni fotosito. "M", in pratica, è un attributo variabile di ogni fotosito. Questa condizione è chiamata Non-Uniformità di Risposta ai Pixel (PRNU) . Considerando questo, sostituiremo il fattore "M" con "Mp": useremo la desinenza "p" come indicazione che "M" varia per ogni fotosito su ogni data posizione del sensore "p". ADU p = M p ⋅ EL + RNS

Dobbiamo notare come le variazioni di sensibilità di "Mp" non sono determinate, ma sono cambiamenti casuali da fotosito a fotosito. In questo senso, "Mp" è una variabile casuale rispetto alla superficie del sensore. Questo fatto è rappresentato con l'uso del carattere in grassetto per "Mp". Tuttavia, considereremo che ogni sito, nel corso del tempo, ha sempre il suo stesso valore "Mp". Questo significa che "Mp", per ogni fotosito, è una costante nel tempo (tra uno scatto e l'altro) quando si mantiene la stessa velocità ISO (la sensibilità del fotosito cambia con la velocità ISO). Il valore medio (ovvero, statisticamente parlando, il valore atteso) di tutti i fattori "Mp", corrispondente a tutti i fotositi nella superficie del sensore, è una costante. Questa media è probabilmente l'obiettivo perseguito dal processo di produzione. Chiameremo "EM" ( E xpected M ultiplier) a questa media: EM = Eva( M p )

Modelleremo "Mp" come variazioni intorno a questa media. A tal fine, considereremo "Mp" come composto da due componenti additivi (questo è plausibile considerando questa formula per l'Eva() della somma di due variabili): una è la media "EM" e l'altra è la deviazione di sensibilità del fotosito rispetto a tale media. Chiameremo "MDp" a quest'ultimo componente (per la deviazione "M"): M p =EM + MD p

Si noti che questo modo di esprimere "Mp" implica che la media di "MDp" è pari a zero ( Eva(MDp) = 0 ). Possiamo sondare questo applicando l'operatore del valore atteso a entrambe le estremità dell'equazione precedente e utilizzando "Eva(EM) = EM" (giustificato da questa formula per l'Eva() di una costante): M p =EM + MD p Eva( M p )= Eva(EM + MD p ) = Eva(EM) + Eva( MD p ) EM = EM + Eva( MD p ) Eva( MD p ) = EM - EM = 0 Aggiornando il nostro modello del sensore nella formula dell' ADU p , otteniamo ADU p = M p ⋅ EL + RNS = (EM + MD p ) ⋅ EL + RNS - μ RNS

Le tre sorgenti di rumore, rappresentate con caratteri in grassetto, sono indipendenti l'una dall'altra. Questo ci permetterà di utilizzare formule più semplici per ottenere il valore atteso e la varianza dell'ADU risultante. Valore medio e variazione spaziale di ADU Il valore medio spaziale dell'ADU Per ottenere il valore atteso del fotosito (stimato in base al loro valore medio) nel nostro modello, applicheremo l'operatore del valore atteso a entrambe le estremità della nostra equazione del modello. Useremo questa equazione anche per il Valore Previsto di un prodotto di variabili indipendenti per ottenere: Eva( ADU p ) = Eva((EM + MD p ) ⋅ EL ) + Eva( RNS ) - μ RNS = Eva(EM + MD p ) ⋅ Eva ( EL ) + Eva( RNS ) - μ RNS = (Eva(EM + Eva( MD p ) )⋅λ +μ RNS - μ RNS = EM⋅λ

La Variazione spaziale del valore dell'ADU Per ottenere la variazione (spaziale) -nel nostro modello- useremo questa equazione per la varianza di un prodotto di variabili indipendenti tra quelle che abbiamo già utilizzato. All'inizio, otteniamo queste equazioni, dove i termini con valore zero sono mostrati "cancellati". Var( ADU p ) = Var((EM + MD p ) ⋅ EL ) + Var ( RNS ) + Var( μ RNS ) = EM²⋅ Var( EL ) + Var ( MD p )⋅ Var( EL ) + Var ( MD p )⋅ (Eva( EL ))² + Var ( EL )⋅ (Eva( MD p ))² + RN²

Come notazione, ci riferiremo alla varianza di "MDp" come "PRNU²". In questo modo il termine per il rumore PRNU è "PRNU". Si noti che il simbolo dell'equazione "PRNU" si riferisce alla deviazione standard delle sensibilità dei fotositi (in ADU/e-) e non al rumore che questo PRNU causerà nell'immagine grezza (in ADU). Var(MD p ) == PRNU StdDev(MD p ) == PRNU Utilizzeremo anche le seguenti equazioni, già spiegate: Var(EL) = λ Eva(EL) = λ Eva (MD p ) = 0 La varianza risultante è: Var( ADU p ) =Var ( MD p ) ⋅ λ² + (EM² + Var( MD p )) ⋅ λ + RN² = PRNU² ⋅ λ² + (EM² + PRNU²) ⋅ λ + RN²

Questa è l'equazione che stavamo cercando dall'inizio di questa sezione. Dal modello del sensore è nata una semplice equazione che spiega il profilo di rumore, direttamente leto alle caratteristiche del sensore. Si noti come la varianza sia un polinomio quadratico di λ, che rappresenta il conteggio medio degli elettroni nei siti fotosensibili. Il termine quadratico è la sinergia tra il rumore di PRNU e il rumore fotonico. Oltre al termine quadratico, il PRNU ha anche un impatto nel termine lineare λ, tutto questo ci dice che la varianza di sensibilità tra i fotositi (PRNU) può essere una fonte molto forte di rumore. Il rumore (deviazione standard) è solo la radice quadrata della varianza nella formula di cui sopra. In questo modo, il SNR è: Il limite PRNU SNR Se il PRNU fosse l'unica fonte di rumore nel sensore, la varianza totale dell'ADU sarebbe principalmente il termine quadratico della varianza che abbiamo trovato sopra. In tal caso sarebbe SNR: Si noti che questo SNR è indipendente dal conteggio degli elettroni. Questo è anche il limite massimo di SNR se consideriamo tutti e tre i tipi di rumore come nella formula 13. Più formalmente: se il valore di λ nella formula di cui sopra continua a crescere, l'SNR risultante rimarrà sempre al di sotto del valore SNR_PRNU che abbiamo trovato in precedenza. Fortunatamente, per la maggior parte dei sensori delle fotocamere DSLR, il rumore PRNU inizia a dare fastidio vicino al limite superiore di λ (ad esempio 16.383 ADU per i file raw a 14 bit) e non causa danni eccessivi a SNR solo perché la gamma λ termina prima. Le tre fasi del rumore nel SNR Nel grafico qui di seguito riportiamo una curva SNR simulata, dove possiamo distinguere le tre fasi che mostrano la dominanza di ogni tipo di rumore che abbiamo studiato fino ad ora. All'estremità sinistra della curva, con bassi valori di ADU (nell'area mostrata con sfondo arancione) il rumore di lettura rende SNR leggermente più in basso rispetto alla linea tratteggiata grigia che rappresenta il sensore ideale, con solo rumore di lettura e di scatto. Nella seconda parte (con sfondo verde), l'SNR è dominato dal rumore di lettura e "rimane" con una pendenza di circa 0,5. All'estremità destra (sfondo viola), l'SNR rallenta il suo tasso di crescita e inizia a piegarsi, per rimanere asintoticamente sotto il limite PRNU, indicato con una linea tratteggiata rossa. Un semplice modello matematico per il sensore della DSLR Ogni fotosito del sensore della fotocamera è sensibile, principalmente, a uno solo dei componenti a colori RGB (rosso, verde e blu) che comporranno l'immagine finale. L'immagine seguente descrive in modo semplice ma significativo come il sensore della fotocamera DSLR colleziona la luce che lo colpisce in valori pixel RGB in unità ADU. La luce che colpisce il sensore durante il tempo di esposizione è composta da fotoni. Quando ogni fotone raggiunge un particolare strato sul sensore di silicio , il fotone produce un elettrone. L'unità per una quantità di elettroni è "e-". Una volta terminato il tempo di esposizione, l'ADC (convertitore analogico/digitale A/D) nel circuito del fotosito "conta" quanti elettroni sono in ogni fotosito e converte il conteggio in ADU. In questa quantizzazione di elettroni, diremo, l'ADC utilizza un fattore di conversione "M" (da Moltiplicatore), con l'unità "ADU/e-", per moltiplicare la somma di elettroni e ottenere il valore di ADU corrispondente. Prima dell'inizio dell'esposizione, tutti i fotositi vengono risistemati in modo da iniziare l'esposizione con il conteggio degli elettroni impostato a zero. La velocità "M" dipende solo dall'impostazione della velocità ISO della fotocamera. Per valori ISO più alti, "M" sarà più alta, richiedendo meno elettroni per fare un ADU, con conseguente sensore più sensibile alla luce come previsto. Il flusso dei fotoni che colpiscono ciascun sito è proporzionale all'intensità della luce che li genera. In questo modo, come previsto, le aree più scure della scena fotografata corrisponderanno a un basso conteggio di elettroni e di conseguenza a bassi valori di ADU, mentre le aree più chiare corrisponderanno a valori di ADU più elevati. Rappresenteremo il conteggio degli elettroni in ogni fotosito, alla fine del tempo di esposizione, con il simbolo "EL" (per ELettroni) e utilizzando l'unità e- . Quindi, il nostro modello per il sensore è: ADU = M ⋅ L

Rumore di scatto o rumore del fotone (o fotonico) Fino a questo punto del nostro modello, a prima vista sembra che non abbiamo ancora una sorgente di rumore, ma l'abbiamo già, ed è il conteggio degli elettroni rappresentato da "EL". Anche con un'illuminazione perfettamente uniforme, il numero di elettroni in ogni fotosito, dopo l'esposizione, non è lo stesso. Questo conteggio invece di una costante è una variabile casuale; quei diversi valori sulla superficie dell'immagine sono il tipo di rumore chiamato Photon Shot Noise (Rumore di scatto del fotone). Per capire questo, immaginiamo un sacco di tazze identiche poste sotto una pioggia uniforme e che alla fine della pioggia nessuna tazza è stata riempita fino all'orlo. Se dopo la pioggia controlliamo le tazze, scopriremo che la quantità di pioggia raccolta in ogni tazzina non è molto diversa dalle altre. Ma se lo misuriamo in modo molto preciso, troveremo diverse quantità di pioggia in ogni tazza. Qualcosa di simile accade con i fotoni che colpiscono i fotositi. Una spiegazione più formale è che anche se il flusso di fotoni è costante e uniforme sopra il sensore, la quantità di fotoni che colpiscono ogni fotosito e producono elettroni non è una costante, ma una variabile casuale a seguito di una distribuzione Poisson perché l'arrivo di quei fotoni seguire un processo di Poisson. Un processo Poisson è ( da Wikipedia ) definito come "u n dato numero di eventi discreti che si verificano in un intervallo fisso di tempo e/o spazio, dove questi eventi si verificano con una velocità media nota e indipendentemente dal tempo trascorso dall'ultimo evento ". Nel nostro caso, gli eventi discreti sono lo scatto di fotoni che producono elettroni, e "in un tempo e in uno spazio determinati" corrisponde al tempo di esposizione su ogni superficie del sito, ad un ritmo che è effettivamente indipendente da qualsiasi fotone precedente arrivato. E' consuetudine rappresentare la media e la varianza della distribuzione di Poisson con la lettera greca lambda " λ ". Per cui nelle successive equazioni "λ" rappresenterà il valore atteso e la varianza del conteggio degli elettroni in ogni fotosito. Come numero di elementi, tecnicamente λ è adimensionale. Tuttavia, per rendere più comprensibili le equazioni, viene utilizzato con l'unità immaginaria ADU quando rappresenta il valore atteso o rumore (deviazione standard) e ADU² quando rappresenta la varianza. Se valutiamo il valore atteso per entrambi i lati dell'equazione otteniamo: Var (ADU) = Var (M ⋅ EL) = M² ⋅ Var (EL) = M² ⋅ λ

Ora, se si sostituisce "λ" in quest'ultima equazione con la precedente nella formula del Valore Previsto, si ottiene: Var (ADU) = M ⋅ Eva (ADU)

Nota: Queste ultime equazioni sono tutte sovra-semplificazioni del modello di rumore del sensore, a prescindere da altre sorgenti di rumore che includeremo più avanti. Nonostante ciò, sono ancora utili per mostrare il il rumore del fotone in quanto di fatto ha una distribuzione Poisson, perché questa sorgente di rumore è la principale componente di rumore nei nostri dati. La formula di cui sopra indica che nell'ipotesi in cui il rumore abbia una distribuzione di Poisson, la varianza di luminosità dell'immagine (il quadrato del rumore) avrà una relazione lineare con il suo Valore Atteso. Se il Rumore di Fotone fosse l'unica fonte di rumore nell'immagine, l'SNR sarebbe la radice quadrata del conteggio medio degli elettroni raccolti (la radice quadrata di lambda "λ" nelle equazioni seguenti). Notate che questo è un limite imposto da una proprietà fisica della luce. Un rumore del sensore di una telecamera può essere valutato rispetto a questo limite sapendo che il suo SNR non può essere migliore di questo. Nelle equazioni seguenti, ricordate che il rumore è la radice quadrata della varianza. L'ultima equazione rappresenta l'SNR di un sensore ideale per telecamera, dove l'unica sorgente di rumore proviene dalla natura della luce e non c'è altra sorgente di rumore. Quando l'SNR è espresso in modo logaritmico, il rumore di scatto (o del fotone) SNR viene rappresentato come una linea con pendenza di ½. Se prendiamo logaritmi ad entrambe le estremità dell'equazione di cui sopra, otteniamo: Come riassunto, possiamo dire circa il rumore di scatto: È proporzionale alla luminosità media della radice quadrata. Ciò significa che la sua varianza cresce linearmente con la luminosità (o segnale). Ha una distribuzione Poisson, che per luminosità superiore a 1.000 ADU è molto simile alla distribuzione Normale. Il suo SNR cresce con la luminosità della radice quadrata. Il rumore dell'immagine Il rumore dell'immagine è un picco casuale di variazione della luminanza - in ciascuno dei canali RGB - in luoghi in cui ci si aspetta che sia uniforme o che possa cambiare gradualmente. È più evidente nelle aree scure e quando l'immagine viene ingrandita o attentamente ispezionata a livello di pixel. Il rumore può essere descritto come composto da " rumore di luminanza " e " rumore di colore ", dove il "rumore di luminanza" è il rumore che mantiene sostanzialmente la stessa tonalità complessiva, mentre nel "rumore di colore" (chiamato anche "rumore di croma") ci sono anche cambiamenti nella tonalità. Tuttavia, poiché il rumore è un cambiamento casuale nei canali RGB, la sua presenza in un'immagine grezza comporta sempre entrambi i tipi di rumore. Oltre alle intenzioni creative o estetiche, il rumore del colore è quasi sempre indesiderabile. Tuttavia, il rumore di luminanza non è necessariamente una caratteristica indesiderata dell'immagine, a volte è necessario per evitare un aspetto posterizzato o plastificato dell'immagine finale. Poiché il rumore è una variazione della luminanza, è meglio misurarlo con la statistica della deviazione standard, che misura la quantità di variazione dei valori rispetto alla propria media. D'ora in poi, quando ci riferiamo alla quantità di rumore, parleremo della Deviazione Standard (solitamente rappresentata con la lettera greca sigma " σ ") della luminosità lungo la superficie dell'immagine. A sua volta, la deviazione standard è la radice quadrata della varianza , che viene rappresentata come sigma al quadrato " σ² ". In altre parole, il rumore è anche la radice quadrata della varianza. La visione umana può risolvere i cambiamenti di luminosità quando questi sono superiori all'1% circa. Mettendo da parte il valore, in questo modo rilevare le variazioni di luminosità sulla base di un rapporto di contrasto, significa che lo stesso rumore è più evidente quando la luminosità media è più bassa ed è meno evidente quando la luminosità media è più alta. Ciò implica che il modo migliore per misurare l'impatto visivo del rumore è considerare la proporzione tra il rumore e la luminosità media dell'area dell'immagine contenente il rumore. Il modo "classico" per esprimere questa proporzione è attraverso il rapporto segnale/rumore (di solito abbreviato come S/N o SNR) che è anche la luminosità media divisa per la quantità di rumore (deviazione standard). Poiché la luminosità media e la deviazione standard sono indicate entrambe in ADU (Analogico-Digitale: un'unità di misura senza dimensione, i valori dei pixel immagine grezzi sono indicati in ADU), il rapporto SNR è senza dimensione. È implicito che la Media e la Deviazione Standard siano calcolate tra i pixel della stessa immagine, su un'area dove tutti i pixel dovrebbero avere la stessa luminosità. SNR = valore medio Luminosità Pixel / Deviaz. Standard Luminosità Pixel = Media/Rumore

Poiché il rumore è un cambiamento casuale e lo misuriamo con la deviazione standard, è facile capire perché l'uso di statistiche èutile per analizzarlo. Nella pratica approssimeremo il valore di luminosità atteso (indicato con Eva() ) con la luminosità media del campione di immagine e la deviazione standard sarà ottenuta dalla varianza del campione di immagine (indicata con Var() ). Calcoleremo questi valori statistici dai dati grezzi dell'immagine, dove i valori dei pixel sono in unità ADU. Poiché il rapporto segnale/rumore può avere una gamma molto ampia di valori, lo stesso viene normalmente espresso dal suo logaritmo. Questo può essere un logaritmo di base 2, nel qual caso si dice che l'SNR è espresso in stop . SNR_Stop = Log₂(SNR) = Log₂(Media/Rumore)

Il rapporto SNR è spesso espresso in decibel (dB), nel qual caso è calcolato come 20 volte il logaritmo base 10 dell'SNR.

SNR_dB = 20⋅Log₁₀(SNR) = 20⋅Log₁₀(Media/Rumore)

Nella tabella seguente sono riportate le categorie SNR che, secondo il DxO Mark, possono essere considerate come un riferimento per i livelli di rumore buoni, scadenti e cattivi. Sono espressi nelle tre forme: il rapporto stesso, in stop e in dB. Naturalmente i confini tra categorie contigue sono sfumati e sembrano sovrapporsi. Categoria Rumore Rapporto Stops dB Buono quando superiore a 80 6.3 38 Accettabile quando superiore a 40 5.32 32 Non accettabile da e superiore 10 3.32 20 Cattivo quando inferiore a 10 3.32 20 Una variazione di 6 dB corrisponde approssimativamente ad un fattore 2 rispetto all'SNR. Ad esempio, si noti nella tabella precedente, che quando l'SNR in dB cambia da 38 a 32 (6 dB) l'SNR cambia da 80 a 40, il che corrisponde effettivamente ad un fattore di due. Lo stesso avviene da 32dB a 20dB: c'è una differenza di 2⋅6dB = 12dB, corrispondente al doppio del fattore 2 (2⋅2 = 4), e corrispondentemente l'SNR scende da 40 a 10 (40/10 = 4). Nella seguente figura ( la parte a sinistra ) sono mostrati gli esempi di rumore come descritti nella tabella di cui sopra. Per evitare che la correzione gamma distorca l'SNR desiderato, è necessario fare qualche espediente: le immagini vanno preparate in sRGB lineare e poi convertite in sRGB senza modificare l'aspetto delle immagini stesse. Durante la modifica dell'immagine occorre fare attenzione a non far cadere SNR, ad esempio aggiungendo contrasto nelle aree ombreggiate rumorose. Se in uno spazio lineare si alza semplicemente l'intera luminanza dell'immagine moltiplicandola per un dato fattore, l'SNR non cambia: se M e N sono i livelli medi e di rumore attuali, l'SNR corrente è M/N . Alzando tutti i livelli di luminosità attraverso una linea con pendenza f si cambia la luminosità in " f⋅M ". Tuttavia l'SNR non cambierà, perché il rumore cambierà anche in " f⋅N ". Nel software di elaborazione delle immagini grezze, questo tipo di regolazione viene effettuata con il controllo "Correzione dell'esposizione". SNR = (f⋅M)/(f⋅N) = M/N

Abbiamo visto come una curva di tono e/o una correzione gamma implicite sono applicate (a volte automaticamente e inevitabilmente) sulla luminosità lineare dell'immagine grezza nel software di elaborazione delle immagini e questo può interagire con la nostra modifica delle immagini e abbassare inaspettatamente l'SNR. SNR non è l'unico fattore da considerare per quanto riguarda il rumore. L'SNR è importante quasi quanto la sua frequenza spaziale: due immagini possono avere lo stesso SNR, una con rumore di piccole dimensioni, uniformemente scintillato sopra l'immagine (più alta frequenza spaziale) e l'altra con rumore composto da pezzi di diversa luminosità (più bassa frequenza spaziale). Chiaramente il secondo tipo di rumore è peggiore del primo. L'esempio è riportato nella figura di sopra ( sezione destra ). Un occhio umano sano, a seconda delle condizioni ambientali (che determinano la dimensione della pupilla), può risolvere da 50 o 60 cicli per grado (cy/deg) fino a circa 100 cy/deg, come mostrato nel seguente grafico che mostra la media della frequenza cardiaca media dell'occhio umano ( Journal of Vision ). Ricordiamo che l'occhio umano inizia a risolvere il contrasto da circa l'1%, ecco perché il "guadagno" inizia a 0,01. Per una data distanza di visione possiamo ottenere la dimensione del ciclo necessario al calcolo della frequenza spaziale utilizzando la seguente formula (un ciclo viene standardizzato a due pixel immagine su schermo o punti quando viene stampato) Lunghezza_ciclo = 2⋅Distanza⋅Tan(gradi_per_ciclo/2)

Supponiamo di avere un'immagine con un rumore caratteristico di 50 SNR. Supponiamo anche che questo rumore ha una dimensione di 1,7 pixel. Questo significa cicli di 3,4 pixel/ciclo. Se si stampa quell'immagine a 600 dpi, ogni ciclo avrà una lunghezza di (25.4mm/pollice)/(600pixel/pollice)⋅3.4pixel/ciclo = 0.144 mm/ciclo. A una distanza di osservazione di 45 cm, questi cicli sono a una frequenza spaziale di 54,6 cicli/grado (calcolati utilizzando il contrario della formula di cui sopra). Se guardiamo la media MTF dell'occhio umano, con un'apertura pupillare di 4mm (per esempio) troveremo per 54.6 cicli/grado un guadagno di 0.04 circa. Ciò significa che un rumore con un rapporto di contrasto di 1:50 (50 SNR) sarà attenuato a 0,04:50 (il guadagno è 0,04), "corrispondente" a un rumore di 62 dB, che non sarà visto dall'osservatore. Ora possiamo capire come la risoluzione di presentazione dell'immagine (pixel/mm), la distanza di visualizzazione, la dimensione del rumore, l'intensità del rumore (SNR) e l'ambiente di visualizzazione (dimensione della pupilla) siano fattori importanti per determinare l'impatto del rumore nell'immagine visualizzata. Per complicare ulteriormente il soggetto, la risposta dell'occhio umano alla frequenza spaziale è diversa per la luce monocromatica e bianca. La norma ISO 15739:2013 "Fotografia - Immagini fisse elettroniche - Misurazioni del rumore" (originale: "Photography - Electronic still-picture imaging - Noise measurements") specifica come effettuare le misurazioni del rumore della fotocamera tenendo conto di tutti i fattori summenzionati. Questo articolo è focalizzato sulle caratterizzazioni del rumore della fotocamera DSLR, i suoi componenti e la loro relazione matematica. E' come se considerassimo sempre lo scenario peggiore in cui il rumore esistente è chiaramente visibile, come con un guadagno di 1 MTF. Isolamento del rumore PRNU dall'immagine Possiamo isolare il rumore PRNU dell'immagine facendo una media di una serie di scatti identici di una superficie illuminata uniformemente, leggermente sfuocata, e con impostazioni di sovraesposizione piuttosto elevate, ma facendo attenzione a non ottenere valori di highlight tagliati nell'immagine grezza. In questo modo faremo in modo da ottenere una maggiore presenza del rumore PRNU su ogni immagine. Si noti che questa media non è come prima su tutta la superficie dell'immagine ma limitata allo stesso pixel. Si noti che qui stiamo parlando del rumore nell'immagine (in ADU) causato dalla sensibilità non costante dei fotositi (PRNU). Per sottolineare questo, stiamo usando l'espressione "rumore PRNU d'immagine". Non confondete quindi questo con il "PRNU" usato nelle precendenti equazioni, che rappresenta la Deviazione standard delle sensibilità del fotosito del sensore (in ADU/e-). La media dell'immagine farà risaltare il rumore PRNU, perché (per un dato pixel) non cambia da scatto a scatto. Tuttavia, gli altri tipi di rumore (di lettura e di scatto), che cambiano casualmente da scatto a scatto, diminuiscono nella media. Lo vedremo più chiaramente dalla formula seguente. <img class="mathtex-equation-editor aligncenter" src="http://chart.apis.google.com/chart?cht=tx&chl=%5Cfrac%7B%5Csum%20%7BADU_p%7D%7D%7Bn%7D%20%3D%20%5Cfrac%7B%5Csum%20((EM%20%2B%20MD_p)%5Ccdot%20EL%2BRNS-%5Cmu_%7BRNS%7D)%7D%7Bn%7D%20%3D(EM%2BMD_p)%5Ccdot%20%5Cfrac%7B%5Csum%20%7BEL%7D%7D%7Bn%7D%2B%5Cfrac%7B%5Csum%20%7BRNS%7D%7D%7Bn%7D-%5Cfrac%7B%5Csum%20%7B%5Cmu_%7BRNS%7D%7D%7D%7Bn%7D%0A%0A" alt="frac{sum {ADU_p}}{n} = frac{sum ((EM + MD_p)cdot EL+RNS-mu_{RNS})}{n} =(EM+MD_p)cdot frac{sum {EL}}{n}+frac{sum {RNS}}{n}-frac{sum {mu_{RNS}}}{n} " align="absmiddle" /> In questa formula, poiché stiamo facendo la media dello stesso pixel in un insieme di immagini grezze, le somme vengono fatte per ogni pedice "p" fisso. Questo è il motivo per cui possiamo considerare "MDp" dalla somma nella prima equazione. Il numero di immagini medie è rappresentato da "n". Se applichiamo l'operatore della varianza su entrambe le estremità dell'equazione di cui sopra, otterremo: <img class="mathtex-equation-editor" src="http://chart.apis.google.com/chart?cht=tx&chl=Var%20(%5Cfrac%7B%5Csum%20%7BADU_p%7D%7D%7Bn%7D)%3DEM%5E2%5Ccdot%5Cfrac%7B%5Csum%20Var(EL)%7D%7Bn%5E2%7D%2B%5Cfrac%7B%5Csum%20var(%5Cmu_%7BRNS%7D)%7D%7Bn%5E2%7D%2Bvar%20(MD_p)%5Ccdot%20%5Cfrac%7B%5Csum%20Var(EL)%7D%7Bn%5E2%7D%2Bvar%20(MD_p)%5Ccdot%20(%5Cfrac%7B%5Csum%20Eva(EL)%7D%7Bn%5E2%7D)%5E2%0A%0A" alt="Var (frac{sum {ADU_p}}{n})=EM^2cdotfrac{sum Var(EL)}{n^2}+frac{sum var(mu_{RNS})}{n^2}+var (MD_p)cdot frac{sum Var(EL)}{n^2}+var (MD_p)cdot (frac{sum Eva(EL)}{n^2})^2 " align="absmiddle" /> Alla fine otterremo la seguente equazione: Nell'equazione precedente si può vedere come il termine quadratico PRNU non sia influenzato dalla media, mentre l'impatto degli altri tipi di rumore diminuisce con valori "n" maggiori, il numero di immagini mediate. Come prova, abbiamo scattato 32 foto con l'obiettivo della fotocamera che puntava un telone liscio monocromatico. Le immagini grezze risultanti hanno valori di pixel verdi all'87% del loro limite superiore. In altre parole, sono sovraesposti ma non vanno oltre il loro limite superiore. Per mostrare l'effetto di questa media sulla varianza dell'immagine risultante, il grafico seguente mostra la risultante del rumore di ogni immagine sul fotosito (deviazione standard) e anche il rumore dall'immagine risultante dalla media di un diverso numero di fotografie. Ogni foto contiene una varianza aggiuntiva che non proviene dal rumore, ma per la vignettatura dell'obiettivo. Per questo motivo il grafico sopra riportato mostra i dati di un'area di campionamento di 46 x 66 pixel, scelta per essere un'area di immagine uniformemente illuminata. Il rumore dell'immagine media diminuisce molto marginalmente a partire da circa 20 campioni. Se tracciamo una linea dal centro dell'immagine ad uno dei suoi angoli e tracciamo i valori dei pixel lungo quella linea, otterremo la curva mostrata nel grafico seguente, dove i cambiamenti (spaziali) ad alta frequenza nei valori dei pixel sono causati -principalmente- dal rumore PRNU. La vignettatura è la causa della curva di tendenza generale con la forma dell'arco. Per isolare il rumore PRNU dell'immagine dalla vignettatura dell'obiettivo, ci siamo sbarazzati di quella forma ad arco e abbiamo ottenuto il rumore PRNU "oltre" una linea piatta. 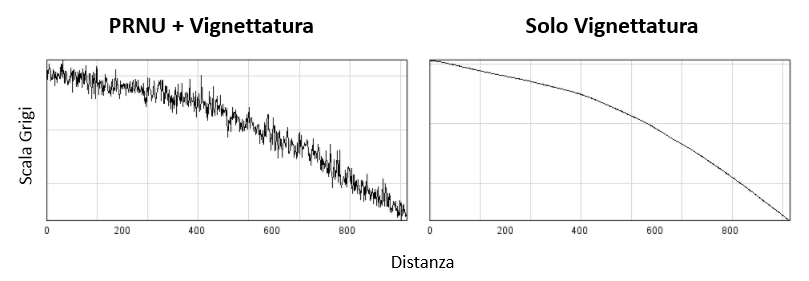Un modo per rimuovere la vignettatura dell'obiettivo è usare una tecnica chiamata Correzione del campo piatto . In generale, la correzione del campo piatto richiede la sottrazione di una "cornice scura" per rimuovere il rumore di lettura ed eventualmente altri tipi di rumore del sensore (ad esempio il rumore termico). Tuttavia, per le fotocamere Nikon (come abbiamo già visto), il file immagine grezzo viene fornito con questa correzione già fatta per il rumore di lettura e non abbiamo il rumore termico che deriva da esposizioni di più secondi, né lo abbiamo considerato in questo corso. In primo luogo, si de-rumorerà l'immagine media, applicando alcuni filtri Photoshop (forte riduzione del rumore e alcune sfocature gaussiane), al fine di rimuovere le variazioni ad alta frequenza e ottenere solo lo sfondo con la vignettatura dell'obiettivo, chiameremo "campo piatto" per l'immagine risultante. Per effettuare la correzione del campo piatto, dividiamo ogni valore di pixel nell'immagine media per quello corrispondente (con le stesse coordinate di posizione nel sensore) nell'immagine a campo piatto (pixel per pixel, usando il software ImageJ) e poi moltiplichiamo il risultato per il valore di pixel mediano in quel campo piatto. pixel(prnu, x, y) = [pixel(immagine_media, x, y)/pixel(campo_piatto, x, y)] * mediano(campo_piatto)

Dove pixel(img, x, y) è una funzione che permette di ottenere o impostare il valore del pixel con coordinate (x,y) nel file immagine "img". L'immagine che ne deriva è quella qui sotto, contenente solo il rumore PRNU. La metà di sinistra mostra il rumore dell'immagine PRNU al 100% della scala. La metà di destramostra un'altra parte del rumore PRNU dell'immagine ma con una scala del 50%, cosa che rende più evidente un pattern verticale, ma mostra anche che c'è un pattern orizzontale. Come si può vedere, il rumore PRNU nella dimensione spaziale non è totalmente casuale, probabilmente può essere decomposto in tre parti: colonna , riga e un residuo casuale dovuto alle componenti spaziali. Rimozione (della maggior parte) del rumore dell'immagine PRNU Un modo per rimuovere gran parte del rumore PRNU dell'immagine è quello di scattare la differenza - pixel per pixel - di due immagini identiche. Scattiamo due foto identiche con scene, illuminazione e impostazioni della fotocamera identiche. Notate che nella nostra nomenclatura, il termine PRNU è la deviazione standard delle sensibilità dei fotositi, che a sua volta causa rumore nell'immagine chiamata rumore immagine PRNU. L'idea è che essendo il PRNU causato da un termine (MDp) che rimane costante tra scatti identici, saremo in grado di rimuoverlo nella differenza di queste due immagini. Utilizzeremo l'operatore delta "Δ" per indicare la differenza dei valori rispetto allo stesso pixel in due scatti identici. Il delta del μRNS, come delta di un valore costante, è pari a zero. ADU p = (EM + MD p ) ⋅ EL + RNS - μ RNS

Δ ADU p = (EM + MD p ) ⋅ Δ EL + ΔRNS - Δμ RNS

Poiché "MDp" è una caratteristica del fotosito e non cambia tra uno scatto e l'altro, è possibile eliminare il termine dall'operatore delta. Ora applichiamo l'operatore di varianza (spaziale) a entrambi i lati dell'ultima equazione. Alla fine otterremo: var(Δ ADU p ) = EM²⋅Var( Δ EL ) + Var( MD p )⋅ Var(Δ EL ) + Var ( MD p )⋅ (Eva(Δ EL ))² + Var (Δ EL )⋅ (Eva( MD p ))² + 2⋅ RN²

I termini eliminati hanno valore zero. Alla fine, otterremo la seguente equazione: var(Δ ADU p )/2 = (EM² + PRNU²) ⋅ λ + RN²

Si noti che il lato destro dell'equazione sopra riportata è simile alla formula della varianza ADUp ma - come si voleva - non include il termine quadratico della varianza PRNU. Anche quando include il termine lineare PRNU (in "λ"), la varianza PRNU (PRNU²) è di solito molto più piccola del termine "EM²". Come conseguenza pratica di ciò possiamo ignorare il termine PRNU² e considerare che il risultato contiene solo il rumore di scatto e di lettura. La formula di sopra ci dice che se calcoliamo la differenza di immagine tra due scatti identici e la dividiamo per la radice quadrata di 2, l'immagine risultante conterrà - principalmente - solo il rumore di scatto e di lettura. Riepilogo delle formule di Modellazione del rumore del sensore Abbiamo sviluppato alcune formule per modellare il valore del pixel grezzo dell'immagine e le sue statistiche. Durante questo sviluppo abbiamo mostrato molte equazioni intermedie spiegando in dettaglio come abbiamo ottenuto le equazioni finali principali . Riassumiamo ora le principali equazioni alle quali siamo giunti e che ci serviranno in tutti i futuri discorsi circa il rumore sul sensore di una fotocamera digitale. Il valore del pixel immagine grezza Il valore del pixel in un file immagine grezzo può essere descritto come: ADU p = M p ⋅ EL + RNS = (EM + MD p ) ⋅ EL + RNS - μ RNS

dove "EM" è il rapporto medio utilizzato dal sensore per convertire il numero di elettroni in unità di valore di pixel (ADU) in ogni fotosito. Il termine "MD p " rappresenta le deviazioni di sensibilità del fotosito intorno al loro valore "EM" e la somma di questi due termini è il rapporto utilizzato per il fotosito per la conversione del suo numero di elettroni in unità ADU. Il conteggio degli elettroni nel fotosito è rappresentato da "EL". I termini "EM" e "MD p " sono indicati in unità "ADU/e-", mentre "EL" è in "e-". (elettroni). In questo modo il risultato del prodotto è "ADU". Il termine "RNS" è l'errore sistematico di lettura del rumore, che possiamo definire "segnale finto", aggiunto dalla circuiteria del sensore al "segnale reale", ed è dato in unità ADU. Il termine μRNS (anche in ADU) è il valore medio di quella distorsione del "segnale finto" di rumore di lettura, che viene sottratto dalla lettura del fotosito per rimuoverlo. Dobbiamo distinguere due diversi effetti del rumore di lettura: Aggiunge un errore sistematico ai valori del fotosito aumenta la loro varianza. La correzione del rumore in lettura rimuove la distorsione nei valori dei siti foto, ma anche se la varianza aggiunta rimane nell'immagine. La seguente equazione descrive il valore atteso della lettura del fotosito del sensore da un'area dell'immagine, corrispondente a una superficie uniformemente illuminata che causa lo stesso flusso di elettroni su ciascun fotosito. Qui stiamo supponendo che non ci sia caduta di luce causata, per esempio, dalla vignettatura dell'obiettivo. Lo stesso contesto si applica alla formula della varianza che mostriamo qui di seguito. Stimiamo questo Valore Previsto attraverso la media aritmetica dei valori dei pixel dell'immagine grezza. Eva( ADU p ) = EM⋅λ

Nell'equazione precedente, "λ" rappresenta il valore atteso del conteggio degli elettroni nei siti fotosensibili. La varianza di valore dei pixel dell'immagine grezza La seguente formula modella la varianza delle letture dei fotositi del sensore da un'area dell'immagine corrispondente a una superficie uniformemente illuminata. Come il conteggio degli elettroni in ogni fotosito - dopo un'esposizione - segue una distribuzione di Poisson, la loro varianza e il loro valore atteso hanno lo stesso valore λ. Abbiamo bisogno della varianza (spaziale) per misurare il rumore. Il rumore viene misurato dalla radice quadrata della varianza: la statistica della deviazione standard dei valori dei pixel dell'immagine grezza. Var( ADU p ) = PRNU² ⋅ λ² + (EM² + PRNU²) ⋅ λ + RN²

Nell'equazione sopra riportata, il termine "PRNU²" è la varianza delle sensibilità deifotositi dei sensori, questa è la varianza di "MD p " nella formula vista sopra (la prima). Non confondetelo con il rumore PRNU dell'immagine che ne deriverà. Il termine "RN²" corrisponde alla varianza del rumore di lettura, che è solo il quadrato della misura di rumore li lettura stesso. La varianza della differenza di due immagini identiche Possiamo misurare il rumore del sensore, con il componente PRNU rimosso, usando la seguente equazione. Var(Δ ADU p ) / 2= (EM² + PRNU²) ⋅ λ + RN² Questa equazione modella la varianza della differenza di due immagini identiche (due fotografie identiche della stessa scena, con impostazioni e illuminazione della fotocamera identiche). Realizzazione di un modello matematico - le formule a supporto Introduzione alle formule Questo è il repository delle formule che usiamo insieme ad altri articoli. Lo scopo di questo documento è quello di avere in modo sintetico, gli operatori matematici e termini con la loro notazione e alcune relazioni utili tra di loro. Non dimostreremo come ottenerli. Ciò esula dal campo di applicazione del presente documento e vi sono molte risorse sul web in proposito. Per la moltiplicazione utilizziamo l'operatore "⋅". In questo modo, se vediamo il termine "abxy", in un'espressione matematica, sappiamo che rappresenta una singola entità e non - per esempio - la moltiplicazione dei termini "ab" per "xy", nel qual caso useremo "ab⋅xy". In queste formule, l'operatore "==" è usato principalmente per mostrare due modi alternativi di esprimere la stessa cosa. Formule Statistiche In queste formule, i simboli con carattere in grassetto (ad esempio X) rappresentano variabili casuali e i simboli con carattere regolare (non in grassetto) rappresentano variabili non casuali (ad esempio "c"). Il valore atteso Si utilizza l'espressione Eva( X ) per indicare il valore atteso della variabile casuale X. Il simbolo μx rappresenta il valore risultante da tale espressione. Eva( X ) == μ x

Il valore atteso di una variabile non casuale, ad esempio una costante, è il valore della variabile non casuale stessa: Eva(a) = a

Il valore atteso del prodotto di due variabili casuali indipendenti è uguale al prodotto di tali variabili: Eva ( X · Y ) = Eva ( X ) · Eva ( Y )

Eva ( X · Y ) = μ x · μ y

Se la variabile è scalata da una costante (una variabile non casuale) il valore atteso viene scalato di tale costante. Si tratta di una conseguenza diretta delle due formule precedenti. Eva (a · X ) = a · Eva ( X )

Se due variabili casuali sono correlate, significa che il valore di una di esse, in qualche misura, determina o influenza il valore dell'altra. La Covarianza è una misura di quanto tali variabili siano correlate. Ad esempio, il fumo è correlato con la probabilità di avere un cancro: più si fuma, maggiore sarà la probabilità di avere un cancro. Il valore atteso del prodotto di due variabili casuali correlate è uguale al prodotto di tali variabili più la loro Covarianza: Eva ( X· Y ) = Cov ( X,Y ) + μ x · μ y

Si noti come la formula 3 sia un caso particolare della formula precedente: quando le variabili casuali sono indipendenti, il termine Covarianza è zero e scompare. Il valore atteso della somma di tutte le variabili casuali è uguale alla somma dei valori attesi di tali variabili. Questo è vero indipendentemente dal fatto che tali variabili casuali siano indipendenti o meno. Eva ( X + Y ) = Eva ( X ) + Eva ( Y ) = μ x + μ y

Il consolidamento delle relazioni precedenti determina la proprietà di Linearità dell'operatore del Valore Atteso (Linearità dell'Attesa), che è vera indipendentemente dal fatto che le variabili casuali siano indipendenti o meno. Eva(a ·X + b · Y + C) = a · Eva( X ) + b · Eva( Y ) + c = a · μ x + b · μ y + c

La covarianza Usiamo l'espressione Cov( X, Y ) per indicare la Covarianza delle due variabili casuali X e Y. Cov ( X , Y ) == σ ( X, Y ) == σ x,y

La Covarianza è una misura di quanto i valori di ciascuna delle due variabili casuali correlate determinano l'altra. Se entrambe le variabili cambiano nello stesso modo (ad esempio quando -in generale- una cresce anche l'altra), la Covarianza è positiva, altrimenti è negativa (ad esempio quando si aumenta l'altra diminuisce). Se le variabili sono indipendenti la Covarianza è zero. Tuttavia, la Covarianza deve essere considerata zero o non zero da un punto di vista statistico, il che significa che c'è qualche fatto che ci porta a credere che il valore di Covarianza non possa essere giustificato solo sulla base del caso. Cov ( X , Y ) = Eva[( X - Eva ( X )) · ( Y - Eva ( Y ))] = Eva [( X -μ x ) · ( Y -μ y )]

Se le variabili sono indipendenti, la loro Covarianza è pari a zero. Questo si può chiaramente vedere nella seguente formula, dove se entrambe le variabili fossero indipendenti l'una dall'altra, entrambi i termini nella sottrazione diventerebbero lo stesso valore e la Covarianza diventerebbe zero: Cov ( X , Y ) = Eva[( X · Y ) - Eva ( X ) · Eva ( Y ) = Eva ( X · Y ) - μ x · μ y

Tuttavia, il contrario della regola precedente non è sempre vero: se la Covarianza è zero, non significa necessariamente che le variabili casuali siano indipendenti. Ad esempio, se X è distribuito uniformemente in [-1, 1], il suo valore atteso e il valore atteso delle potenze dispari (ad esempio X³) di X risultano pari a zero in [-1, 1]. Per questo motivo, se la variabile casuale Y è definita come Y = X², chiaramente X e Y sono correlati. Tuttavia, la loro Covarianza è numericamente uguale a zero: Cov (x,y) = Cov (x,y = x²) = Cov (x, x²) = Eva (x · x²) - Eva (x) · Eva (x²) = Eva (x³) - Eva (x)· Eva (x²) = 0-0· Eva (x²) = 0 La Covarianza è commutativa. Cov ( X , Y ) = Cov ( Y , X )

La Covarianza è invariata allo spostamento di una o entrambe le variabili. Cov ( X + h, Y + k) = Cov ( X , Y )

La Covarianza viene scalata in base a ciascuna delle scale di X e Y. Cov (a · X , b · Y ) = a · b · Cov ( X , Y )

Consolidamento delle ultime due equazioni: Cov (a · X + h, b · Y + k) = a · b · Cov ( X , Y )

La varianza La varianza è il caso particolare della Covarianza quando entrambe le variabili sono uguali Var ( X ) = Cov ( X, X ) == σ ( X, X ) == σ²( X ) ==σ x ²

La varianza misura quanto i valori di una variabile casuale sono sparsi. In altre parole, quanto sono diversi tra loro. Var ( X ) = Eva[( X - Eva ( X ))²] = Eva [(X -μ x )²]

Possiamo calcolare la varianza dai valori attesi di X e del suo quadrato (X²). Var ( X ) = Eva (X²) - Eva²(X) = Eva (X²) - μ x ²

La varianza di una variabile non casuale è zero. Var (a) = 0

La varianza è invariante allo spostamento della variabile. Var ( X + h) = Var ( X )

Se la variabile è scalata da una costante (una variabile non casuale), la varianza viene scalata del quadrato di tale costante. Var (a · X ) = a² · Var ( X )

La varianza della somma o differenza di due variabili casuali correlate è: Var ( X + Y ) = Var ( X ) + Var ( Y ) + 2 · Cov (X,Y ) = σ x ² + σ y ² + 2 · σ x,y

Var ( X - Y ) = Var ( X ) + Var ( Y ) - 2 · Cov (X,Y ) = σ x ² + σ y ² - 2 · σ x,y

Se le variabili sono indipendenti, la Covarianza è zero e la Variazione della somma o della differenza è la stessa: Var ( X + Y ) = Var ( X - Y ) = Var ( X ) + Var ( Y )

La varianza del prodotto di due variabili casuali correlate: Var ( X · Y ) = +Cov ( X², Y² ) + Eva ( X² ) · Eva ( Y ²) - [Cov ( X, Y ) + Eva ( X ) · Eva ( Y )]² = σ x²,y² +μ x² · μ y² -[σ x,y + μ x · μ y ]²

Usando questa relazione tra la varianza e i valori attesi possiamo dire "Eva(X²) = Var(X) + Eva(X)". Usando questo nella formula precedente si ottiene: Var ( X · Y ) = +Cov ( X², Y² ) +[Var( X ) + Eva² ( X ) ] · [Var( Y ) + Eva² ( Y ) ] - [Cov ( X, Y ) + Eva ( X ) · Eva ( Y )]² = σ x²,y² + (σ x ²+μ x ²) · (σ y ²+μ y ²) -[σ x,y + μ x · μ y ]²

La varianza del prodotto di due variabili casuali indipendenti deriva dalle formule precedenti, sapendo che in tal caso σ x,y =σ x²,y² =0: Var ( X · Y ) = Var( X ) · Var( Y ) + Var( X ) · Eva² ( Y ) + Eva² ( Y ) · Var( Y ) = σ x ² · σ y ² + σ x ² · μ y ²+ σ y ² · μ x ²

Un altro modo per ottenere il prodotto di due variabili casuali indipendenti è attraverso questa equazione: Var ( X · Y ) = Eva ( X² ) · Eva ( Y ²) - Eva² ( X ) · Eva² ( Y ) = μ x² · μ y² - μ x ² · μ y ²

Il coefficiente di correlazione Il Coefficiente di Correlazione è una misura della dipendenza tra due variabili casuali -correlate-. <img class="mathtex-equation-editor aligncenter" src="http://chart.apis.google.com/chart?cht=tx&chl=Corr%20(X%2CY)%20%3D%5Cfrac%7BCov%20(X%2CY)%7D%7BStdDev%20(X)%5Ccdot%20StdDev%20(Y)%7D%20%3D%3D%5Crho_%7Bx%2Cy%7D%20%3D%20%5Cfrac%7B%5Csigma%7Bx%2Cy%7D%20%7D%7B%5Csigma_x%5Ccdot%5Csigma_y%7D%20" alt="Corr (X,Y) =frac{Cov (X,Y)}{StdDev (X)cdot StdDev (Y)} ==rho_{x,y} = frac{sigma{x,y} }{sigma_xcdotsigma_y} " align="absmiddle" /> La deviazione Standard Usiamo l'espressione StdDev(X) per indicare la Deviazione Standard della variabile casuale X. StdDev ( X ) == σ( X ) == σ x

La deviazione standard è la radice quadrata della varianza. Relazione analitica tra due funzioni numeriche correlate A volte è possibile misurare due variabili di uscita, da un esperimento, che sono fortemente correlate perché provengono da due funzioni di una variabile comune e ciò che si vuole sapere queste due funzioni. Se si costruisce una formula di correlazione per la relazione tra queste variabili di output, con l'aiuto dei dati di molti esperimenti, è possibile trovare una buona approssimazione di tale formula di correlazione. Tuttavia, la domanda è: Come questa formula di correlazioni può farci luce sulle funzioni che producono quelle variabili di output? Supponiamo, abbiamo f (x) e g (x), entrambi valutati a xi in x1,x2 ....xn, il che significa che abbiamo i punti [f(xi),g(xi)]. Ora troviamo una correlazione su questi punti. La formula di correlazione, tuttavia, naturalmente si situa tra f() e g(). Come possiamo mettere in relazione questa correlazione con f(x) e g(x)? 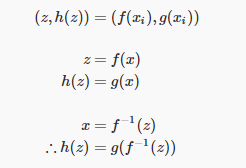Caso lineare Per esempio, vediamo il caso in cui entrambe le funzioni, f() e g(), sono lineari: Ciò significa che quando si correlano due funzioni lineari, la curva risultante è anche una retta, avente come pendenza quella di g(x) divisa per quella di f(x). Sappiamo anche che la retta correlata attraversa l'asse h (quando z=0) con h=(g1/f1)⋅z+(g0-(g1/f1)⋅f0). Possiamo "convalidare" questo caso molto facilmente. Supponiamo che le nostre funzioni lineari lo siano: f ( x ) = 2 ⋅ x + 13 g ( x ) = 3 ⋅ x + 5 Se si tracciano queste funzioni per x in 1,2 si ottiene (f,g)=(15,8),(17,11). Sapendo che questi punti appartengono a una linea, possiamo trovare la pendenza come Δy/Δx. Se la nostra precedente deduzione è corretta, questa pendenza deve essere pari a g1/f1=3/2: pendenza =Δy/Δx=(11-8)/(17-15)=3/2 Questo è esattamente ciò che abbiamo pensato! Anche secondo la nostra ultima formula, l'intercettazione della linea correlata con z=0 dovrebbe avvenire quando h è: h(0) = ( g 1 /f 1 ) · 0 + ( g 0 - ( g 1 /f 1 ) · f 0 ) h= 5 - (3/2) · 13 = -14.5

Possiamo trovare l'intercettazione con z=0 dai dati di linea correlati, sapendo che contiene il punto (15, 8): (h - 8) = (3/2) · (z - 15) = (3/2) · (0 - 15)

h = 8 - (3/2) · 15 = -14.5

Anche in questo caso il risultato è coerente con la nostra deduzione. Caso quadratico Quando f() è lineare ma g() è quadratico, si ottiene: Sviluppando l'ultima equazione e riassumendo, abbiamo finalmente ottenere:

Gli Speciali – La matematica del rumore

Modificare foto su iPhone: 4 applicazioni tra cui scegliere

Paraluce: a cosa servono e ne hai bisogno?

Beppe

Articoli che potrebbero interessarti

Guida definitiva al nudo fotografico: I differenti tipi di fotografia di nudo (con foto)

Guida completa alla fotografia invernale

La guida completa per fotografare il nudo e fare foto di nudo – indice

Le domande da aspettarsi in fase di colloquio: come prepararsi a rispondere

La storia del fotogiornalismo – Dalle origini ai giorni nostri

Come scrivere un curriculum vitae vincente e nel modo corretto

Paraluce: a cosa servono e ne hai bisogno?

Iscriviti alla newsletter

Ultimi Articoli

Fotografare in Digitale

Link Utili

Pubblica le tue foto

Scarica la nostra app

Welcome Back!

Create New Account!

Retrieve your password

Iscriviti alla nostra newsletter

fino al

50% OFF

Hai dato un occhiata ai nostri libri? Solo per un periodo limitato sono disponibili ad un prezzo mai visto!

Are you sure want to unlock this post?

Are you sure want to cancel subscription?

Gli Speciali – La matematica del rumore

Le Fonti del rumore

Rumore di lettura

Support authors and subscribe to content

Buy Article

Modificare foto su iPhone: 4 applicazioni tra cui scegliere

Paraluce: a cosa servono e ne hai bisogno?

Articoli che potrebbero interessarti

Iscriviti alla newsletter

Ultimi Articoli

Fotografare in Digitale

Link Utili

Pubblica le tue foto

Scarica la nostra app

Welcome Back!

Create New Account!

Retrieve your password

Iscriviti alla nostra newsletter

fino al

Are you sure want to unlock this post?

Are you sure want to cancel subscription?