La maggior parte di voi non se ne sarà mai accorta, a parte fotografi, fisici, chimici o chiunque abbia un occhio estremamente acuto, ma i bordi delle immagini sono da sempre un po’ morbidi. Possiamo vedere con estrema nitidezza e chiarezza al centro dell’immagine, sia che si tratti di una macchina fotografica o di un microscopio, ma i lati dell’immagine non sono mai stati così nitidi. Fino ad ora, visto che finalmente possiamo dire di avere la soluzione al problema dell’aberrazione sferica.
E questo perché un fisico e dottorando messicano del Tecnológico de Monterrey, Rafael G. González-Acuña, ha appena risolto il problema matematico di 2.000 anni fa.
Antichi problemi con le lenti
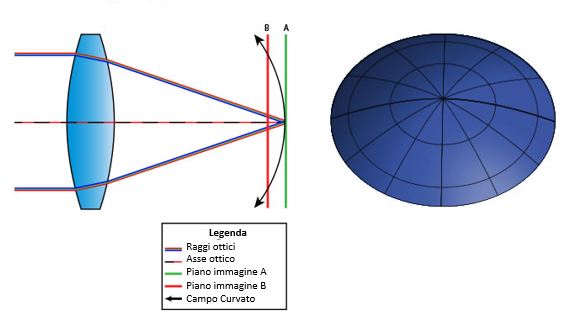
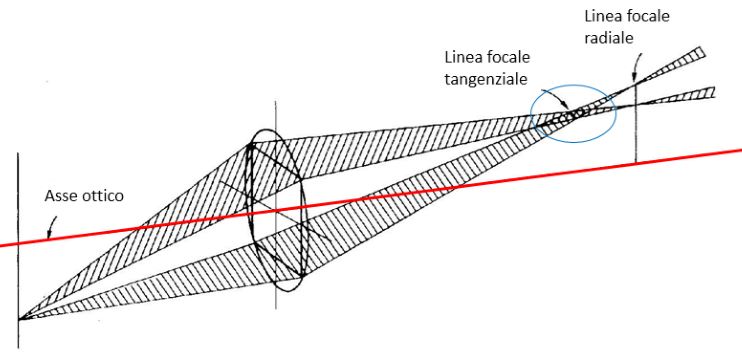
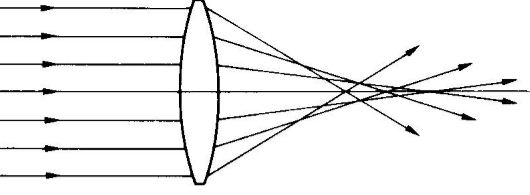
Il problema delle lenti poco chiare non è legato al fatto chela lente sia sporca o sfocata, ma si tratta di un fenomeno ottico chiamato aberrazione sferica. L’aberrazione è un difetto dei sistemi ottici, che rendono l’immagine formata da una lente sfocata o distorta, e la natura di tale distorsione dipende dal tipo di aberrazione.
Un sistema di imaging ottico che presenta un’aberrazione produce un’immagine sfocata. Questo è quando i produttori di strumenti ottici devono correggere i dispositivi per compensare l’aberrazione.
L’aberrazione sferica è un tipo di aberrazione presente nei sistemi ottici che utilizzano superfici sferiche, come macchine fotografiche, telescopi, binocoli, microscopi e così via. Le lenti e gli specchi curvi di questi apparecchi sono generalmente realizzati con superfici sferiche, perché questa forma è più facile da formare rispetto alle superfici curve non sferiche. I raggi luminosi che colpiscono una superficie sferica fuori centro vengono rifratti o riflessi più o meno di quelli che colpiscono vicino al centro. Questa deviazione riduce la qualità delle immagini prodotte dalle apparecchiature ottiche.
Ad oggi, i produttori di lenti sono stati estremamente vicini a creare un’immagine perfetta e uniforme, minimizzando notevolmente l’effetto dell’aberrazione sferica. Tuttavia, queste correzioni costano una montagna di soldi e non sono ancora del tutto perfette.
Ma adesso, con la scoperta di González-Acuña, le cose dovrebbero migliorare in maniera drastica.
La soluzione al problema dell’aberrazione sferica (Wasserman-Wolf, 1949)
Una lente asferica è una lente le cui superfici non sono una porzione di una sfera, ma hanno una forma più libera, ad esempio, l’obiettivo di una macchina fotografica.
Una lente asferica può ridurre o eliminare l’aberrazione sferica e ridurre altre aberrazioni ottiche come l’astigmatismo, rispetto ad una semplice lente sferica. Una singola lente asferica può spesso sostituire un sistema multi-lente molto più complesso. Il dispositivo risultante è più piccolo e leggero e a volte più economico del design a lenti multiple.
Nella progettazione di sistemi ottici, la superficie asferica mira a ridurre fortemente l’aberrazione sferica. Molti autori hanno proposto una lente con due superfici asferiche per correggere l’aberrazione sferica, ma di per sé tutte le soluzioni sono di natura numerica.
Il problema della progettazione di una lente senza aberrazione sferica è noto anche come il problema Wasserman-Wolf, postulato da Wasserman e Wolf nel 1949 in un articolo pubblicato su Royal Society Proceedings, che tecnicamente spiega il problema, ma non fornisce una soluzione analitica (va comunque detto che già nel 1690 si parla di questo problema).
La soluzione, come detto, è adesso alla portata di tutti e potete trovare i dettagli nel seguente articolo: General formula for bi-aspheric singlet lens design free of spherical aberration.
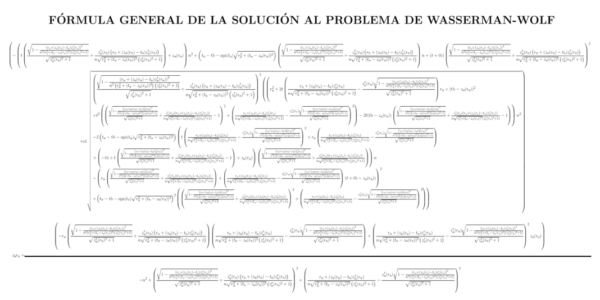
Figure 1Questa formula conclude sette decenni di ricerca della soluzione dell’aberrazione sferica, nota anche come problema Wasserman-Wolf. Fonte: Rafael G. González-Acuña/Tecnológico de Monterrey
In questa equazione vengono definiti i parametri di una seconda superficie della lente tale da correggere tutta l’aberrazione generata dalla prima superficie, in modo tale che l’aberrazione sferica venga eliminata. Lo scienziato ha calcolato l’efficienza della lente su un campione di di 500 raggi: questa è stata pari al 99,9999999999999999%. Questa scoperta può avere molte applicazioni, in quanto ci permetterà di produrre obiettivi con una qualità d’immagine superiore a qualsiasi distanza, spessore e materiale.
La soluzione del problema Levi-Civita (1900)
D’altra parte, il problema generale degli ovali cartesiani fu considerato per la prima volta dal fisico matematico italiano Levi-Civita nel 1900, senza dare una formula analitica per la risoluzione. Il problema dell’ovale cartesiano generalizzato è quello di trovare una superficie refrattiva che trasformi un fronte d’onda in entrata in un fronte d’onda sferico in uscita.
In una pubblicazione presentata insieme ai ricercatori Alejandro Chaparro Romo e Julio Gutiérrez Vega nella rivista Applied Optics, sotto il titolo ” General formula to design freeform singlet free of spherical aberration and astigmatism“, viene finalmente data una risposta analitica a questo antico problema, anch’esso un problema per le lenti fotografiche.
In sintesi, entrambe le soluzioni presentate dal team di ricercatori hanno un enorme potenziale nella progettazione di dispositivi ottici, e le loro applicazioni sono molteplici, in particolare nella progettazione di lenti, macchine fotografiche, microscopi, telescopi, endoscopi, ecc, che si caratterizzano per l’elevata qualità dell’immagine.
soluzione al problema dell’aberrazione sferica: Le conseguenze
L’equazione offre una soluzione analitica per contrastare l’aberrazione sferica. Da ora, i produttori di lenti potranno usare questa formula che offre un modello esatto per creare una lente otticamente perfetta – nitidezza costante da una parte all’altra.