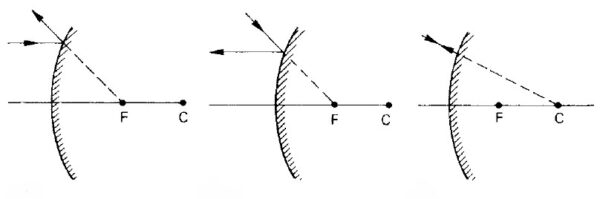
La rifrazione da una lente può essere determinata se i percorsi di alcuni dei raggi formanti l’immagine sono tracciati mediante semplici oggetti grafici, ovvero linee. Ora, per poter semplificare al massimo la rappresentazione grafica di una lente e dei raggi che la attraversano, bisogna identificare delle regole generiche che, applicandole, ci semplifichino la vita senza farci discostare troppo (approssimazione) dal risultato reale. Per una lente positiva, quattro sono le regole che generalmente possiamo prendere in considerazione, ovvero:
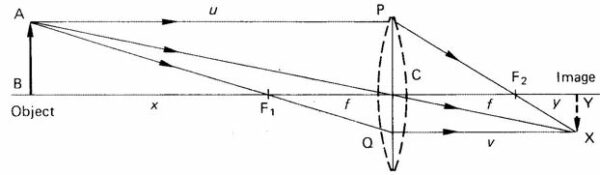
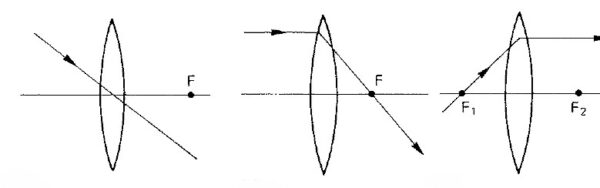
- Un raggio passante per il centro di una lente sottile non è deviato
- Un raggio che colpisce la lente parallelamente all’asse ottico, passa attraverso un punto focale della lente sul lato opposto della stessa (dopo aver subito la rifrazione all’interno della lente stessa)
- Un raggio passante per il punto focale di una lente, dopo la rifrazione all’interno della lente stessa, emerge dalla lente parallelamente all’asse ottico.
- Un raggio meridionale (ovvero un raggio posizionato su di un piano contenente l’asse ottico) entrato nella piano nodale anteriore ad un’altezza X rispetto all’asse ottico, emerge dal piano nodale posteriore alla stessa altezza X rispetto all’asse ottico, sullo stesso lato e non deviato.
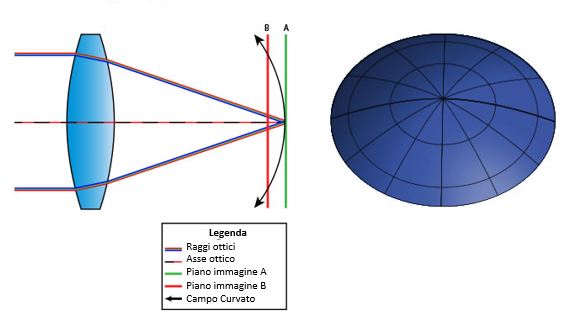
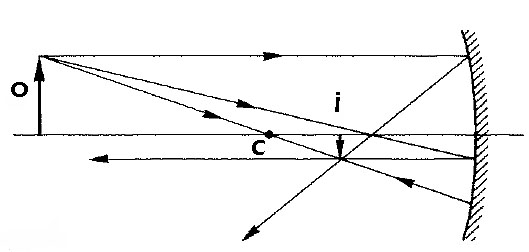
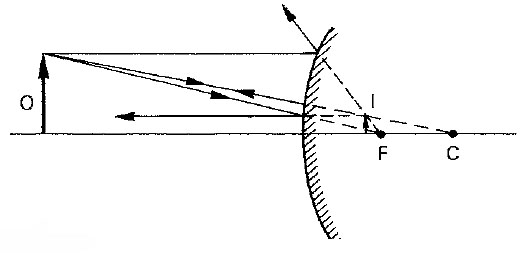
Queste regole (tranne l’ultima) sono illustrate nella Figure qui di seguito:
L’equazione della lente coniugata
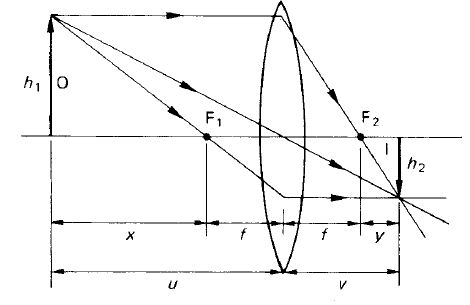
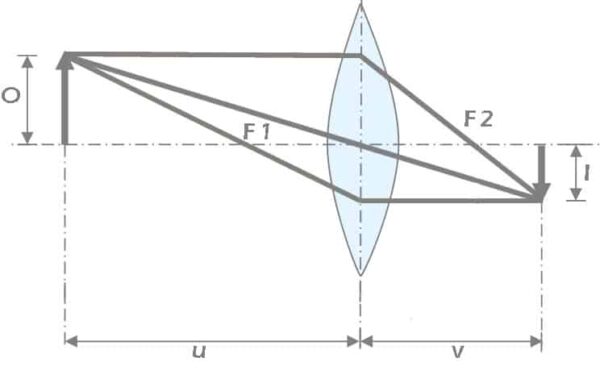
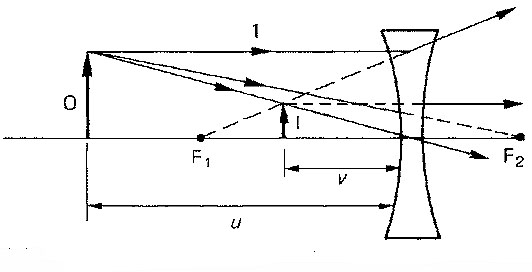
Una relazione può essere ricavato tra le distanze coniugate e la lunghezza focale di una lente. Facendo riferimento alla figura qui di seguito, una lente positiva della lunghezza focale f con una distanza dell’oggetto pari ad u forma un’immagine alla distanza v.
Da triangoli simili ABC e XYC, abbiamo: AB/XY = BC/YC = u/v. E sempre osservando la figura, possiamo ricavare il valore di BF1 : BF1 = u – f. Analizzando inoltre i triangoli simili ABF e QCF abbiamo che: BF1/CF1 = AB/QC = AB/XY
Sostituendo le prime due equazioni nella terza, otteniamo
risistemando la formula e dividendo per uf, otteniamo la formula della lente coniugata:
Questa equazione può essere applicata alle lenti spesse se u e v sono misurate dai punti cardinali appropriati. L’equazione non è al contrario molto adatta per l’uso fotografico pratico in quanto non tiene in considerazione le dimensioni dell’oggetto AB o dell’immagine XY (normalmente una delle due dimensioni è nota).
Definendo l’ingrandimento (m) come XY/AB = v/u e sostituendo nell’equazione della lente coniugata quest’ultima, si ottiene (ri-arrangiando la formula):
e anche
v = f ( 1 + m )
A causa della relazione coniugata tra u e v (come mostrato nella formula di sopra), tali distanze sono spesso chiamate la distanza dell’oggetto coniugato e distanza dell’immagine coniugata.
Da notare inoltre che per la maggior parte degli scopi fotografici elementari è possibile applicare una convenzione per la quale le distanze tra gli oggetti reali e le immagini reali sono considerate come positive. Tutte le distanze tra gli oggetti reali e le immagini virtuali sono considerate come negative. L’ingrandimento di un’immagine virtuale è anch’essa negativa.
Di seguito, infine potete trovare un piccolo compendio delle formule relative ai coniugati in alcuni casi tipici (sempre ovviamente semplificati).
Lente Semplice
Nel caso di lente semplice valgono le seguenti formule:
1 / u + 1 / v = 1 / f e anche: h2 / h1 = I / O = v / u = m
ricalcolando per u e v otteniamo:
e
nel caso u fosse pari ad infinito o nel caso in cui u fosse molto più grande di v, possiamo considerare v = f e quindi m = f / u. Infine, ricordo che x*y=f*f
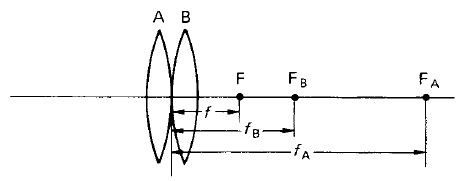
Lenti sottili in contatto
nel caso di due lenti sottile in contatto, abbiamo le seguenti formule (dove P è ial potenza espressa in diottrie):
1 / f =1 / fA + 1 / fB oppure 1 / f = P = Pa + Pb
Lenti sottili separate
nel caso le lenti sottili fossero separate da una leggera distanza, abbiamo